Coding
PriorityQueue 优先队列
第k大的元素
题目:给定一个数组nums和一个整数k,输出数组中第k大的元素
Input: nums = [3, 2, 1, 5, 6, 4], k = 2 |
解法:最小堆 什么是 heap
1. 初始化一个大小为 k 的最小堆,将前 k 个元素加入堆中 |
import heapq |
class Solution { |
前k个元素的频率
题目:给定一个数组nums和一个整数k,返回数组中出现频率最高的前k个元素
Input: nums = [1, 1, 1, 2, 2, 3], k = 2 |
解法 1: heapq.nlargest(Python)
1. 使用 `Counter` 统计元素出现频率 |
from collections import Counter |
解法 2:最小堆
1. 统计元素频率,使用堆存储前 k 个高频元素 |
from collections import Counter |
class Solution { |
解法 3:桶排序
1. 统计频率,并将元素按频率存储在“桶”中 |
from collections import Counter |
class Solution { |
最小堆: 更灵活,可以适应动态输入数据,适合k较小的情况桶排序: 更高效,尤其是当k较大或频率分布较均匀时
Design
LRU 缓存
题目:实现一个数据结构LRU Cache (Least Recently Used Cache),它能够在固定容量下缓存键值对,同时满足以下两种操作get(key): 如果键存在,返回其值,并将该键标记为最近使用。如果不存在,返回-1put(key, value): 插入新键值对。如果缓存已满,移除最久未使用的键值对
解法 1: OrderedDict(Python)Python中的OrderedDict可以非常直观地实现LRU CacheOrderedDict自动维护插入顺序,最久未使用的元素总在最前面- 提供了
move_to_end(key)方法,可以将某个键移动到末尾,表示最近使用
get 方法 |
from collections import OrderedDict |
解法 2: Map(Javascript)JS的Map数据结构,它按插入顺序存储键值对- 使用
set(key, value)方法更新键时,会将该键移到末尾,表示最近使用
get 方法 |
class LRUCache { |
实现随机集合
题目:设计一个支持以下操作的集合,在平均时间复杂度为O(1)下实现插入、删除和随机获取操作insert(val): 如果集合中没有该值,则插入remove(val): 如果集合中存在该值getRandom(): 随机返回集合中的一个元素,每个元素被返回的概率相等
Input |
解法:数组 + 哈希表
1. 数组存储集合的元素,用于随机访问 |
import random |
class Solution { |
LinkedList 链表
反转链表
题目:给定一个单链表的头节点head,将其完全反转,并返回新的头节点
Input: head = [0,1,2,3] |
解法: Two Pointers双指针
1. 初始化两个指针:prev 表示前一个节点,curr 表示当前节点 |
class Solution: |
class Solution { |
反转链表中间部分
题目:给定一个单链表的头节点head,以及两个整数left和right,反转链表中从位置left到位置right的部分,并返回链表的头节点
Input: head = [1,2,3,4,5], left = 2, right = 4 |
解法:虚拟头节点法
1. 添加虚拟头节点:用于处理从链表头部开始反转的特殊情况 |
class Solution: |
class Solution { |
- 例子,反转链表
1 -> 2 -> 3 -> 4 -> 5第2个节点到第4个节点
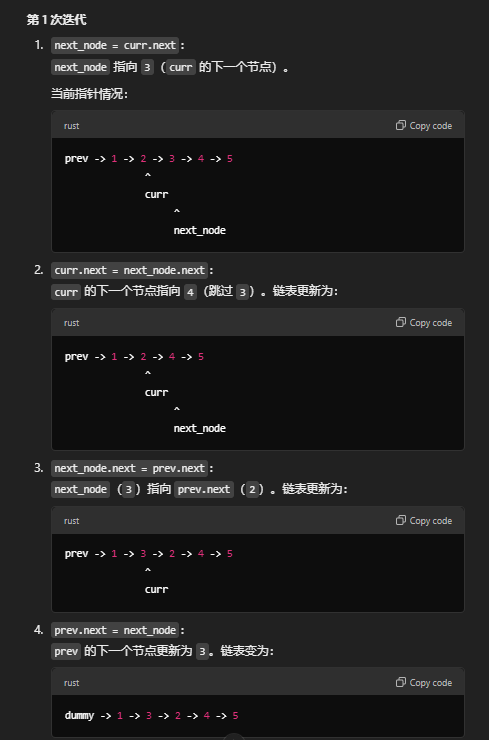
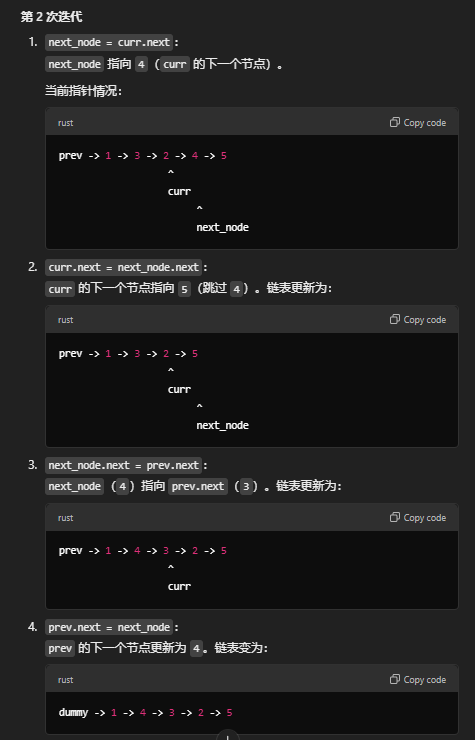
合成链表
题目:给定两个单链表list1和list2,它们的元素按升序排列。将它们合并为一个新的链表,要求新链表也按照升序排列,并返回新链表的头节点
Input: list1 = [1,2,4], list2 = [1,3,5] |
解法:虚拟头节点法
1. 使用一个虚拟头节点 dummy 来简化链表连接逻辑 |
class Solution: |
class Solution { |
k个一组翻转链表
题目:给定一个单链表的头节点head和一个整数k,将链表按照每k个节点为一组进行翻转。如果剩余节点不足k个,则保持原样。要求返回翻转后的链表
Input: head = [1,2,3,4,5,6], k = 3 |
解法:按组翻转 + 双指针
1. 遍历链表并按 k 个节点为一组分割 |
class Solution: |
class Solution { |
成对反转链表节点
题目:给定一个单链表的头节点head,将链表中的节点两两交换,并返回交换后的链表。如果链表节点数是奇数,最后一个节点保持不变
Input: head = [1,2,3,4] |
解法:虚拟头节点法
1. 使用一个虚拟头节点 dummy,便于操作头节点及其后的节点 |
class Solution: |
class Solution { |
对折链表
题目:给定一个单链表head,要求在原地修改链表,不使用额外的空间, 将其重新排序为- 原链表的第一个节点 -> 最后一个节点 -> 第二个节点 -> 倒数第二个节点 ->
Input: head = [1,2,3,4,5] |
解法:快慢指针 + 反转链表 + 合并链表
1. 找到链表中点 |
class Solution: |
class Solution { |
删除有序链表重复元素
题目:从一个升序排列的链表中,删除所有重复的节点,确保每个值只出现一次
Input: head = [1,1,2,3,3] |
解法:遍历链表
1. 从链表头开始,依次检查当前节点和下一个节点的值 |
class Solution: |
class Solution { |
删除有序链表所有重复元素
题目:从一个升序排列的链表中,删除所有出现次数超过1次的节点,仅保留没有重复的节点
Input: head = [1,2,3,3,4,4,5] |
解法:双指针 + 虚拟头节点
1. 创建虚拟头节点 dummy,以处理可能需要删除头节点的情况 |
class Solution: |
class Solution { |
链表转树
- 题目: 将一个有序链表转换为高度平衡的二叉搜索树(
BST)。高度平衡指的是树中每个节点的两个子树的高度差不超过1
Input: head = [-10,-3,0,5,9] |
- 解法: 分治法 + 快慢指针
1. 使用快慢指针找到链表的中间节点,将其作为当前树的根节点 |
class Solution: |
class Solution { |
合并k个有序链表
- 题目: 给定
k个有序链表,将它们合并成一个有序链表并返
Input: lists = [[1,4,5],[1,3,4],[2,6]] |
- 解法: 最小堆(优先队列)
1. 将每个链表的头节点加入最小堆 |
import heapq |
class Solution { |
BFS & DFS
海岛问题
- 题目: 给定一个由
'1'和'0'组成的网格,'1'表示陆地,'0'表示水域,计算网格中岛屿的数量。岛屿被水域包围,由相邻的陆地(水平或垂直方向)连接而成
Input: grid = [ |
- 解法
1: 广度优先搜索 (BFS)
1. 遍历网格中的每个位置,找到未访问的陆地节点作为起点 |
from collections import deque |
class Solution { |
- 解法
2: 深度优先搜索 (DFS)
1. 使用递归替代 BFS 的队列逻辑 |
class Solution: |
class Solution { |
Two Pointers 双指针
雨水问题
- 题目: 给定一个非负整数数组
height,表示每个柱子的高度。假设下雨后水只会停留在柱子之间,请计算可以接住的总雨水量
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1] |
- 解法: 双指针
1. 使用两个指针分别从数组的左右两端向中间靠拢 |
class Solution: |
class Solution { |
盛水问题
- 题目: 给定一个数组
height,其中每个元素表示一个竖线的高度,竖线在横轴上的间隔为1。找到两根竖线之间形成的容器能够盛水的最大面积
Input: height = [1,8,6,2,5,4,8,3,7] |
- 解法: 双指针
1. 初始化左右指针,分别指向数组的两端 |
class Solution: |
class Solution { |
一维数组去重
- 题目: 有序数组
nums,需要原地移除重复项,使每个元素最多出现一次
Input: nums = [0,0,1,1,1,2,2,3,3,4] |
- 解法: 双指针
1. 定义 i 指针跟踪去重后数组的最后一个位置 |
class Solution: |
class Solution { |
最接近的三数之和
- 题目: 给定一个长度为
n的整数数组nums和一个目标值target,找到数组中三个数的和,使其最接近目标值。返回这个和
Input: nums = [-1,2,1,-4], target = 1 |
- 解法: 排序 + 双指针
1. 首先对数组进行排序 |
class Solution: |
class Solution { |
三数之和
- 题目: 给定一个包含整数的数组
nums,返回所有不重复的三元组[nums[i], nums[j], nums[k]],使得nums[i] + nums[j] + nums[k] == 0。答案中不能包含重复的三元组
Input: nums = [-1, 0, 1, 2, -1, -4] |
- 解法: 排序 + 双指针
1. 对数组进行排序,便于去重和使用双指针 |
class Solution: |
class Solution { |
四数之和
- 题目: 给定一个由整数数组
nums和一个目标值target,找出所有不重复的四元组[nums[a], nums[b], nums[c], nums[d]],使得nums[a] + nums[b] + nums[c] + nums[d] == target
Input: nums = [1,0,-1,0,-2,2], target = 0 |
- 解法: 排序 + 双指针 + 多层遍历
1. 对数组进行排序,以便后续去重和使用双指针 |
class Solution: |
class Solution { |
找出数组中的重复数字
- 题目: 给定一个包含
n + 1个整数的数组 nums,其中每个整数都在范围 [1, n] 内,且只有一个重复的数字。找出该重复的数字。注意:不能修改数组内容,并且仅使用常数级别的额外空间
Input: nums = [3,1,3,4,2] |
- 解法: 快慢指针(
Floyd判圈算法)
1. 将数组看作链表,nums[i] 指向下一个节点 |
class Solution: |
class Solution { |
Binary Search
最长递增子序列
- 题目: 给定一个整数数组
nums,找到其中最长严格递增子序列的长度
Input: nums = [10,9,2,5,3,7,101,18] |
- 解法: 动态规划 + 二分法优化
1. 动态规划: |
class Solution: |
class Solution { |
Tree 树与二叉树
二叉树层序遍历
- 实现二叉树的层序遍历(广度优先遍历,
BFS) - 从二叉树的根节点开始,按层级顺序逐层访问节点,每层从左到右
3 |
- 解法: 队列实现
BFS
1. 使用 deque 实现队列,初始包含根节点 |
from collections import deque |
class TreeNode { |
树每层的最大值
- 题目: 给定一个二叉树,按层遍历树,返回每一行中的最大值
1 |
- 解法: 广度优先搜索
BFS
1. 使用队列(deque)进行层序遍历(BFS) |
from collections import deque |
class Solution { |
验证二叉搜索树
- 题目: 验证一棵二叉树是否为二叉搜索树(
BST)
二叉搜索树的性质: |
Input: root = [2,1,3] |
- 解法: 递归验证上下界
1. 使用递归检查每个节点的值是否满足二叉搜索树的性质: |
class Solution: |
class Solution { |
二叉树最大差值
- 题目: 找到二叉树中任意节点与其祖先节点值之间的最大差值
- 祖先节点: 从根节点到当前节点路径上的任意节点
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13] |
- 解法: 深度优先搜索(
DFS)
1. 使用递归(DFS)遍历二叉树 |
class Solution: |
class Solution { |
不同二叉搜索树的数量
- 题目: 给定一个整数
n,表示从1到n的节点,计算可以形成的不同二叉搜索树(BST)的数量
Input: n = 3 |
- 解法: 动态规划 (卡特兰数公式)
1. 定义 G[i] 表示由 i 个节点可以构成的不同二叉搜索树的数量 |
class Solution: |
class Solution { |
检查二叉树是否平衡
- 题目: 给定一个二叉树,判断它是否是高度平衡的
- 平衡二叉树的定义是: 二叉树的任意节点的左右子树高度差不超过
1
- 平衡二叉树的定义是: 二叉树的任意节点的左右子树高度差不超过
Input: root = [3,9,20,null,null,15,7] |
- 解法: 深度优先搜索 (
DFS)
1. 使用递归函数 dfs(node) |
class Solution: |
class Solution { |
二叉搜索树第k小的节点
- 题目: 给定一棵二叉搜索树的根节点
root,以及一个整数k,请返回该二叉搜索树中第k小的节点值
Input: root = [3,1,4,null,2], k = 1 |
- 解法: 中序遍历 (
In-order Traversal)
1. 中序遍历二叉搜索树,按升序访问节点值 |
class Solution: |
class Solution { |
二叉树展开为链表
- 题目: 将二叉树展开为链表,要求“就地”修改树的结构,使其变为一个单链表形式,顺序与前序遍历一致
Input: root = [1,2,5,3,4,null,6] |
- 解法: 递归
1. 递归处理左子树和右子树,将它们分别扁平化 |
class Solution: |
class Solution { |
二叉搜索树的最近公共祖先
Leetcode 235. Lowest Common Ancestor of a Binary Search Tree
- 题目: 在一个二叉搜索树(
BST)中,给定两个节点p和q,找到它们的最近公共祖先(LCA)
Input: root = [5,3,8,1,4,7,9,null,2], p = 3, q = 8 |
- 解法: 利用二叉搜索树的性质
1. 从根节点开始遍历 |
class Solution: |
class Solution { |
对称二叉树
- 题目: 判断给定的二叉树是否是对称的。如果一棵树的左子树和右子树是镜像对称的,则这棵树是对称
Input: root = [1,2,2,3,4,4,3] |
- 解法: 递归
1. 如果树为空,返回 True |
class Solution: |
class Solution { |
存在路径总和
- 题目: 给定一个二叉树和一个目标和,判断树中是否存在从根节点到叶子节点的路径,使得路径上的所有节点值相加等于目标和
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 |
- 解法: 深度优先搜索
1. 从根节点出发,递归地检查左右子树 |
class Solution: |
class Solution { |
所有路径总和
- 题目: 给定一个二叉树和一个目标和,返回所有从根节点到叶子节点的路径,使得路径上的节点值之和等于目标和
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 |
- 解法: 深度优先搜索 + 回溯
1. 使用递归深度优先搜索(DFS)遍历二叉树 |
class Solution: |
class Solution { |
Matrix 矩阵
螺旋矩阵
- 题目: 按照螺旋顺序输出矩阵中的所有元素
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] |
- 解法: 逐层遍历
1. 初始化矩阵的边界 |
class Solution: |
class Solution { |
有效数独
- 题目: 给定一个
9x9的数独棋盘,验证该棋盘是否有效- 每行数字不能重复
- 每列数字不能重复
- 每个
3x3方块中的数字不能重复
Input: board = |
- 解法: 哈希表
1. 使用三个哈希表分别记录 |
class Solution: |
class Solution { |
最大岛屿面积
- 题目: 给定一个二维网格
grid,其中0表示水域,1表示陆地,计算网格中最大的岛屿面积。岛屿由上下左右四个方向相连的陆地组成
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0], |
- 解法: 深度优先搜索(
DFS)
1. 遍历整个网格 |
class Solution: |
class Solution { |
Array 数组
轮转数组
- 题目: 给定一个数组,将其元素向右轮转
k位,其中k是非负数
Input: nums = [1,2,3,4,5,6,7], k = 3 |
- 解法: 翻转法
1. 翻转整个数组 |
class Solution: |
class Solution { |
数组转树
- 题目: 将一个有序数组转换为一棵高度平衡的二叉搜索树(
BST)。高度平衡指的是树中每个节点的两个子树的高度差不超过1
Input: nums = [-10,-3,0,5,9] |
- 解法: 递归构建
1. 选择数组的中间元素作为当前子树的根节点。 |
class Solution: |
class Solution { |
合并两个有序数组
- 题目: 将两个有序数组
nums1和nums2合并为一个有序数组,其中nums1有足够的空间存放nums2的元素
Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 |
- 解法: 双指针从后往前合并
1. 设置三个指针 |
class Solution: |
class Solution { |
每日温度
- 题目: 给定一个整数数组
temperatures,表示每天的温度,返回一个数组answer,其中answer[i]是需要等待的天数,直到temperatures[i]之后出现更高的温度。如果没有更高的温度,answer[i] = 0
Input: temperatures = [73,74,75,71,69,72,76,73] |
- 解法: 单调栈
1. 使用栈存储温度的索引 |
class Solution: |
class Solution { |
String 字符串
字符串解码
- 题目: 给定一个编码过的字符串
s,其中包含嵌套的数字和括号结构,例如3[a2[c]],其解码规则为- 数字表示括号内字符串的重复次数
- 解码后输出完整的字符串
Input: s = "3[a]2[bc]" |
- 解法: 栈
1. 使用栈保存当前的字符串和重复次数 |
class Solution: |
class Solution { |
最长无重复子串
- 题目: 给定一个字符串
s,找出其中不含重复字符的最长子串的长度
Input: s = "abcabcbb" |
- 解法: 滑动窗口
1. 使用两个指针 `left` 和 `right` 维护一个滑动窗口,窗口内的字符不重复 |
class Solution: |
class Solution { |
括号匹配
- 题目: 验证一个只包含括号的字符串是否有效
- 所有的左括号必须有对应的右括号
- 左括号必须以正确的顺序闭合
Input: s = "()[]{}" |
- 解法: 栈
1. 用一个栈来保存左括号 |
class Solution: |
class Solution { |
生成括号
- 题目: 给定一个数字
n,生成所有可能的有效括号组合- 左括号数量等于右括号数量,并且任意位置右括号的数量不超过左括号
Input: n = 3 |
- 解法: 回溯法
1. 使用递归来生成括号组合 |
class Solution: |
class Solution { |
比较版本号
- 题目: 给定两个版本号
version1和version2,比较它们的大小- 如果
version1 > version2返回1 - 如果
version1 < version2返回-1 - 如果它们相等,返回
0
- 如果
Input: version1 = "1.2", version2 = "1.10" |
- 解法: 分割和补齐
1. 使用点号分割版本号,将其转换为整数列表 |
class Solution: |
class Solution { |
经典计算器 (无乘除)
- 题目: 实现一个基本的计算器来计算由正整数、
+、-和括号组成的数学表达式的值。表达式中可能包含空格,确保输入合法且结果不会溢出
Input: s = "(1+(4+5+2)-3)+(6+8)" |
- 解法: 栈 + 模拟
1. 定义一个栈,用于存储运算结果和符号 |
class Solution: |
class Solution { |
经典计算器 (有乘除)
- 题目: 实现一个基本的计算器来计算一个字符串表达式的值。表达式仅包含非负整数、
+、-、*、/运算符以及空格
Input: s = "3+2*2" |
- 解法: 栈 + 模拟
1. 使用栈来保存当前的计算结果 |
class Solution: |
class Solution { |
回文子串个数
- 题目: 给定一个字符串
s,计算其中包含多少个回文子串
Input: s = "abc" |
- 解法: 中心扩展法
1. 中心扩展法 |
class Solution: |
class Solution { |
最长回文子串
- 题目: 给定一个字符串
s,找到其中最长的回文子串
Input: s = "babad" |
- 解法: 中心扩展法
1. 回文的中心可以是一个字符,也可以是两个字符之间的间隔 |
class Solution: |
class Solution { |
大数相加
- 题目: 给定两个非负整数
num1和num2,以字符串的形式表示,返回它们的和,结果也用字符串表示。不能直接使用大整数库或将输入直接转换为整数
Input: num1 = "11", num2 = "123" |
- 解法: 模拟逐位相加
1. 从字符串末尾开始,逐位相加,记录进位 |
class Solution: |
class Solution { |
Backtrack 回溯
全排列(无重复元素)
- 题目: 给定一个不包含重复的数组
nums,返回数组的所有可能的排列,不包含重复
Input: nums = [1,2,3] |
- 解法: 回溯算法
1. 初始化一个空路径 path 和一个 used 数组用于标记是否使用过某元素 |
class Solution: |
class Solution { |
全排列(有重复元素)
- 题目: 给定一个可能包含重复数字的数组
nums,返回数组的所有不重复的排列
Input: nums = [1,1,2] |
- 解法: 回溯算法 + 去重
1. 对 nums 排序,使得相同的数字相邻,方便去重 |
class Solution: |
class Solution { |
Dynamic Programming
分割等和子集
- 题目: 给定一个非空正整数数组
nums,判断是否可以将这个数组分割为两个子集,使得两个子集的元素和相等
Input: nums = [1,5,11,5] |
- 解法: 动态规划(背包问题)
1. 目标是找到一个子集,使其和等于总和的一半 |
class Solution: |
class Solution { |
组成目标和
- 题目: 给定一个数组
nums,可以为每个元素加上+或-符号,问有多少种不同的方式使得总和等于目标值target
Input: nums = [1,1,1,1,1], target = 3 |
- 解法: 动态规划
1. 将问题转换为子集问题,设 P 是正号部分,N 是负号部分 |
class Solution: |
class Solution { |
跳跃游戏
- 题目: 给定一个非负整数数组
nums,每个元素表示在该位置上最多可以跳跃的步数。判断是否能够从数组的第一个位置跳到最后一个位置
Input: nums = [2,3,1,1,4] |
- 解法: 贪心算法
1. 初始化变量 maxReach 记录当前能到达的最远位置 |
class Solution: |
class Solution { |
最小跳跃次数
- 题目: 给定一个非负整数数组
nums,每个元素表示在该位置上最多可以跳跃的步数。求从数组的第一个位置跳到最后一个位置所需的最小跳跃次数
Input: nums = [2,3,1,1,4] |
- 解法: 贪心算法
1. 初始化 jumps(跳跃次数),current_end(当前跳跃的边界),farthest(能跳到的最远位置) |
class Solution: |
class Solution { |
买卖股票的最佳时机
- 题目: 给定一个整数数组
prices,其中prices[i]表示某天的股票价格。只允许完成一笔交易(买入和卖出),求最大利润。如果无法获得利润,返回0
Input: prices = [7,1,5,3,6,4] |
- 解法: 贪心算法
1. 初始化最小买入价格为无穷大,最大利润为 0 |
class Solution: |
class Solution { |
股票买卖的最大收益
- 题目: 给定一个数组,
prices[i]表示第i天的股票价格。可以进行多次买卖操作(但必须先卖掉之前的股票后才能再次购买),求能获得的最大利润
Input: prices = [7,1,5,3,6,4] |
- 解法: 贪心算法
1. 遍历价格数组,检查是否存在连续上涨的价格差 |
class Solution: |
class Solution { |
不同路径的数目
- 题目: 一个机器人位于一个
m x n网格的左上角 (起点在(0, 0))。机器人每次只能向下或向右移动一步。网格的右下角在(m-1, n-1)。问有多少条不同的路径可以到达终点
Input: m = 3, n = 7 |
- 解法: 动态规划
1. 定义 dp 数组,dp[i][j] 表示到达网格 (i, j) 的路径数量 |
class Solution: |
class Solution { |
最大连续和
- 题目: 给定一个整数数组
nums,找到具有最大和的连续子数组(至少包含一个元素),返回其最大和
Input: nums = [-2,1,-3,4,-1,2,1,-5,4] |
- 解法: 动态规划
1. 定义 dp[i] 表示以 nums[i] 结尾的最大子数组和 |
class Solution: |
class Solution { |
最长公共子串
- 题目: 给定两个字符串
text1和text2,返回它们最长公共子序列的长度。如果不存在公共子序列,则返回0
Input: text1 = "abcde", text2 = "ace" |
- 解法: 动态规划
1. 定义 dp[i][j]: |
class Solution: |
class Solution { |
Other 其他
二维数组去重
- 题目: 给定一个二维数组,可能包含重复的行,实现一个方法去重,返回去重后的二维数组
matrix = [ |
- 解法
1: 不保留顺序
将每一行转化为不可变类型 |
class Solution: |
class Solution { |
- 解法
2: 保留顺序
使用 Set 跟踪已经处理的行 |
class Solution: |
class Solution { |
斐波那契数列
斐波那契数列的定义是 |
- 解法
1: 递归
按照定义,递归计算每个斐波那契数 |
class Solution: |
class Solution { |
- 解法
2: 动态规划
使用两个变量存储前两个数值,避免重复计算 |
class Solution: |
class Solution { |
| 方法 | 时间复杂度 | 空间复杂度 | 优点 | 缺点 |
|---|---|---|---|---|
| 递归 | O(2^n) | O(n) | 简单易理解,适合小问题 | 性能差,大量重复计算 |
| 动态规划优化空间 | O(n) | O(1) | 高效,占用空间少 | 不保存所有中间结果 |
| 通用迭代 | O(n) | O(n) | 清晰直观,适合扩展 | 占用更多空间 |
整数反转
- 题目: 给定一个
32位有符号整数x,将其数字部分反转- 如果反转后整数溢出(不在
[-2^31, 2^31 - 1]范围内),返回0
- 如果反转后整数溢出(不在
Input: x = 123 |
- 解法: 逐位反转
1. 记录整数的符号(正或负),然后将整数取绝对值,方便处理 |
class Solution: |
class Solution { |
位1的个数
- 题目: 给定一个无符号整数,返回其二进制表示中
1的个数(也称为汉明权重)
Input: n = 11 (二进制表示为 00000000000000000000000000001011) |
- 解法: 位操作
1. 使用按位与 (n & (n - 1)) 消除最低位的 1,直到 n 为 0,统计次数 |
class Solution: |
class Solution { |
快速排序
- 快速排序是一种基于分治思想的高效排序算法,平均时间复杂度为
O(n log n),最坏情况下时间复杂度为O(n^2)。它的基本思想是通过一次排序将待排序数组分割成独立的两部分,其中一部分的所有元素都比另一部分的所有元素小,然后对这两部分分别进行递归排序。
def quicksort(arr): |
冒泡排序
- 冒泡排序是一种简单的排序算法,它通过重复遍历列表,将相邻的元素进行比较并交换,使得每次遍历后最大(或最小)的元素逐步“冒泡”到列表的末尾。冒泡排序的时间复杂度为
O(n²),适用于小规模数据的排序。
def bubble_sort(arr): |
插入排序
- 插入排序是一种简单直观的排序算法,适合处理小规模数据。它的工作原理是构建一个有序序列,对于未排序的数据,在已排序的序列中从后向前扫描,找到相应位置并插入。插入排序的时间复杂度为
O(n²),在数组几乎有序的情况下表现很好,接近O(n)。
def insertion_sort(arr): |
归并排序
- 归并排序是一种经典的分治算法,通过将数组递归地分成两个子数组,分别进行排序,然后合并这两个有序子数组来实现排序。归并排序的时间复杂度为
O(n log n),它具有稳定性且适用于大规模数据的排序。
def merge_sort(arr): |
堆排序
- 堆排序是一种基于二叉堆的数据结构的比较排序算法,时间复杂度为
O(n log n)。堆排序分为最大堆和最小堆,通常使用最大堆来进行升序排序。堆排序具有原地排序的特点,不需要额外的存储空间。
def heapify(arr, n, i): |
深度优先搜索 (DFS) & 广度优先搜索 (BFS)
- 深度优先搜索:
DFS是一种通过深入每一个节点并尽可能深地搜索其子节点的遍历算法。可以使用递归或显式栈来实现。
def dfs_recursive(graph, node, visited=None): |
- 广度优先搜索:
BFS是一种逐层遍历算法,先访问当前节点的所有相邻节点,再继续访问这些相邻节点的相邻节点。BFS通常用队列来实现。
def bfs(graph, start): |
前序,中序,后序
- 前序遍历顺序为:根节点 -> 左子树 -> 右子树
def preorder(root): |
- 中序遍历顺序为:左子树 -> 根节点 -> 右子树
def inorder(root): |
- 后序遍历顺序为:左子树 -> 右子树 -> 根节点
def postorder(root): |





