算法 Algorithm • 上
前言
本读书笔记节选自
krahets大佬编写的《Hello 算法》。勉励自己开始系统的算法学习。
1. 初识算法
当我们听到“算法”这个词时,很自然地会想到数学。然而实际上,许多算法并不涉及复杂数学,而是更多地依赖于基本逻辑,这些逻辑在我们的日常生活中处处可见。
(1)查阅字典
在字典里,每个汉字都对应一个拼音,而字典是按照拼音的英文字母顺序排列的。假设需要查找一个拼音首字母为r的字,通常会这样操作。
- 翻开字典约一半的页数,查看该页首字母是什么,假设首字母为
m。 - 由于在英文字母表中
r位于m之后,所以排除字典前半部分,查找范围缩小到后半部分。 - 不断重复上面两个步骤,直至找到拼音首字母为
r的页码为止。





查阅字典这个必备技能,实际上就是「二分查找」。从数据结构的角度,我们可以把字典视为一个已排序的「数组」。从算法的角度,我们可以将上述查字典的一系列操作看作是「二分查找」算法。
(2)整理扑克
打牌时,每局都需要整理扑克牌,使其从小到大排列,实现流程如下。
- 将扑克牌划分为“有序”和“无序”两部分,并假设初始状态下最左
1张扑克牌已经有序。 - 在无序部分抽出一张扑克牌,插入至有序部分的正确位置。此时最左
2张扑克已经有序。 - 不断循环上面步骤,每一轮将一张扑克牌从无序部分插入至有序部分,直至所有扑克牌都有序。
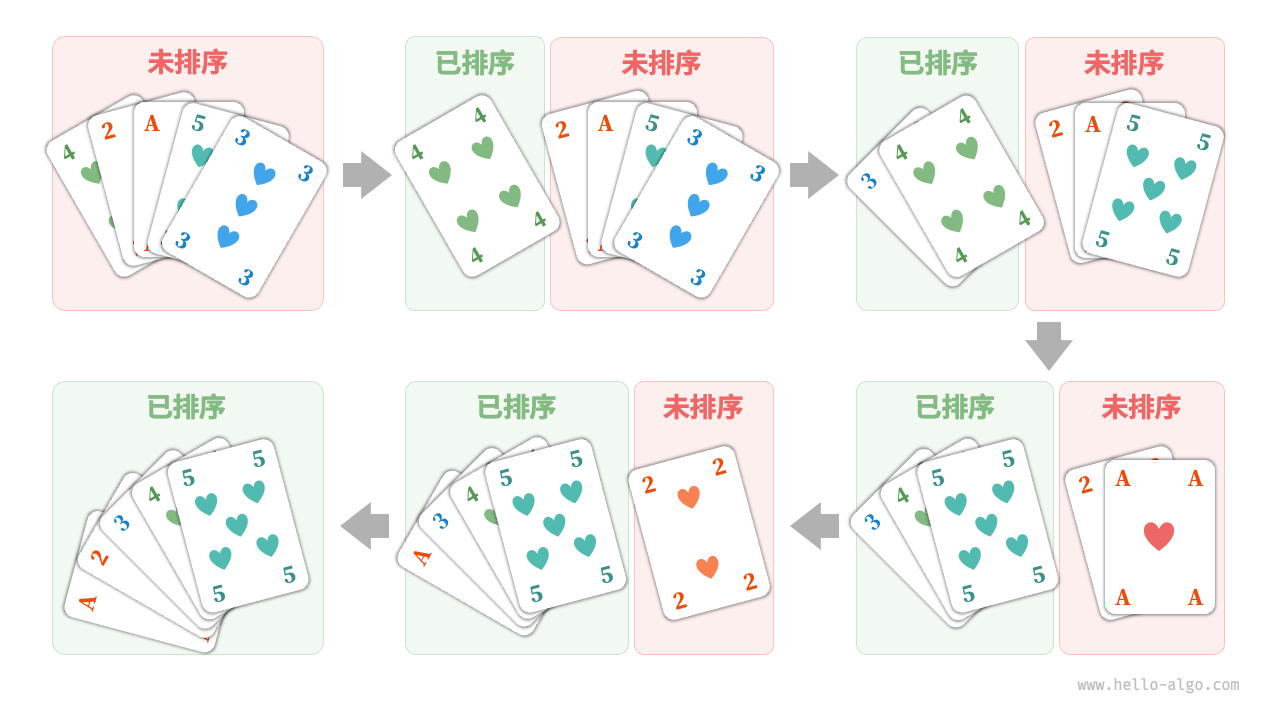
上述整理扑克牌的方法本质上是「插入排序」算法,它在处理小型数据集时非常高效。许多编程语言的排序库函数中都存在插入排序的身影。
(3)货币找零
假设我们在超市购买了69元的商品,给收银员付了100元,则收银员需要给我们找31元。他会很自然地完成以下思考。
- 可选项是比
31元面值更小的货币,包括1,5,10,20元。 - 从可选项中拿出最大的
20元,剩余11元。 - 从剩余可选项中拿出最大的
10元,剩余1元。 - 从剩余可选项中拿出最大的
1元,剩余0元。 - 完成找零,方案为
20 + 10 + 1 = 31元。
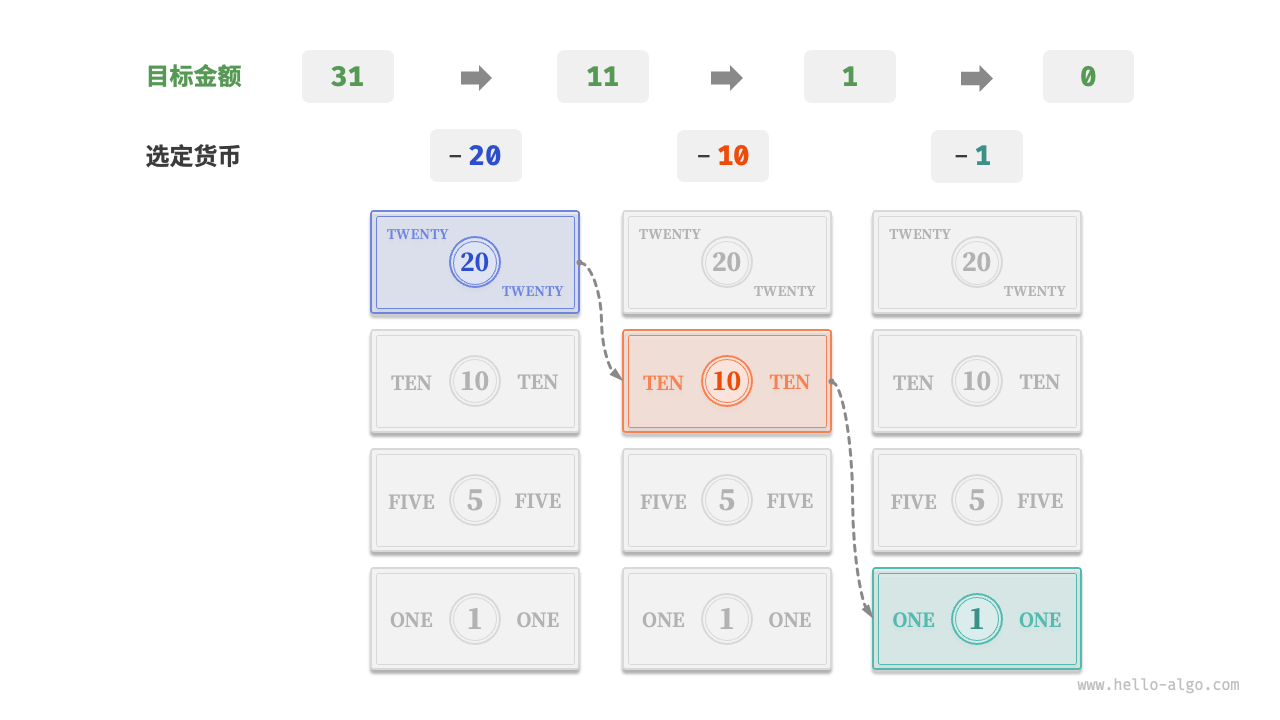
在以上步骤中,我们每一步都采取当前看来最好的选择(尽可能用大面额的货币),最终得到了可行的找零方案。从数据结构与算法的角度看,这种方法本质上是「贪心算法」。
2. 复杂度
2.1 迭代与递归
在数据结构与算法中,重复执行某个任务是很常见的,通常会选用两种基本的程序结构。
「迭代 iteration」是一种重复执行某个任务的控制结构。在迭代中,程序会在满足一定的条件下重复执行某段代码,直到这个条件不再满足。(例如常见的for循环和while循环)
「递归 recursion」是一种算法策略,通过函数调用自身来解决问题。它主要包含两个阶段。
- 递:程序不断深入地调用自身,通常传入更小或更简化的参数,直到达到“终止条件”。
- 归:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
下面代码中,只需调用函数recur(n),就可以完成1 + 2 + ... + n的计算。
/* 递归 */ |

从计算角度看,迭代与递归可以得到相同的结果,但代表了两种不同的思考和解决问题的方式。
- 迭代:从最基础的步骤开始,然后不断重复或累加这些步骤,直到任务完成。
- 递归:将原问题分解为更小的子问题,这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题,直到基本情况时停止。
2.2 时间复杂度
「时间复杂度分析」统计的是算法运行时间随着数据量变大时的增长趋势。下面例子中,假设输入数据大小为n,给定三个算法函数A,B,C。
// 算法 A 时间复杂度:常数阶 |
- 算法
A只有1个打印操作,算法运行时间不随着n增大而增长。此算法的时间复杂度为「常数阶」。 - 算法
B中的打印操作要循环n次,算法运行时间随着n增大呈线性增长。此算法的时间复杂度被称为「线性阶」。 - 算法
C中的打印操作要循环1000000次,虽然运行时间很长,但它与输入数据大小n无关。因此C的时间复杂度和A相同,仍为「常数阶」。
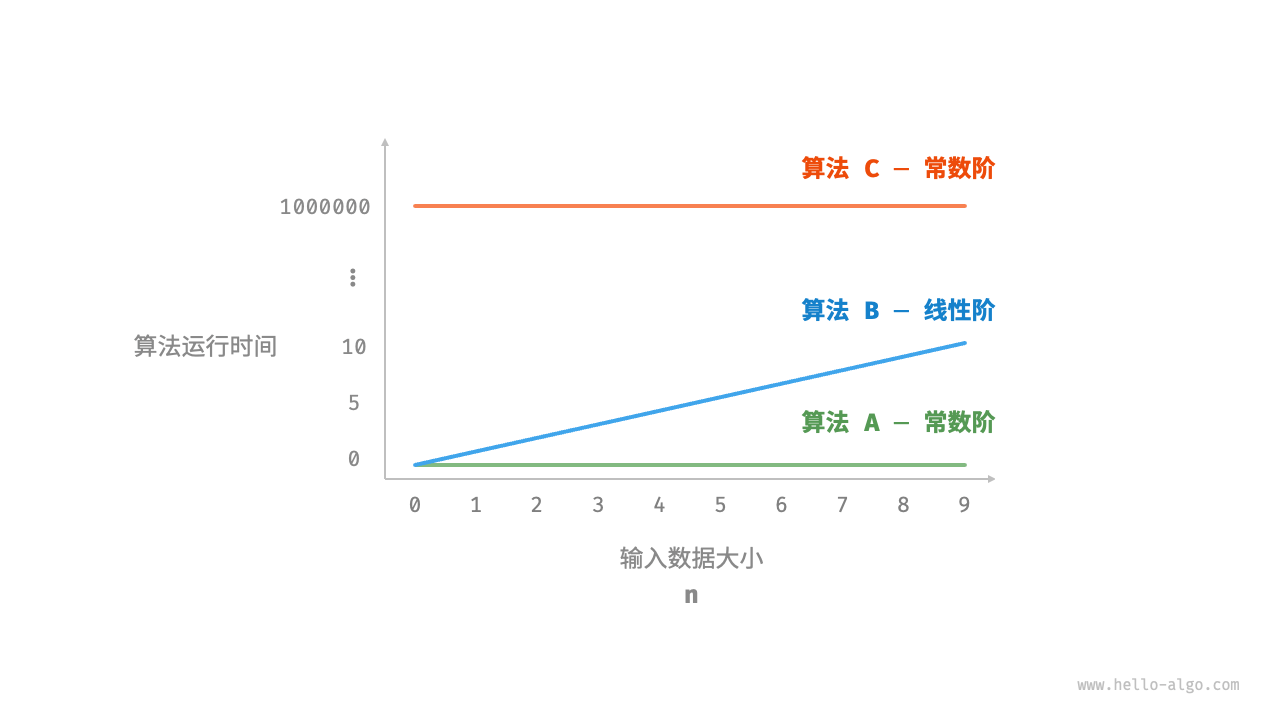
时间复杂度分析有哪些特点呢?
时间复杂度能够有效评估算法效率。算法
B的运行时间呈线性增长,在n > 1时比算法A更慢,在n > 1000000时比算法C更慢。而且只要输入数据大小n足够大,复杂度为“常数阶”的算法一定优于“线性阶”的算法。时间复杂度也存在一定的局限性。算法
A和C的时间复杂度相同,但实际运行时间差别很大。同样,算法B的时间复杂度比C高,但在输入数据大小n较小时,算法B明显优于C。
函数渐近上界
void algorithm(int n) { |
设上面函数的计算操作数量是一个关于输入数据大小n的函数,记为T(n),则其操作数量为T(n) = 3 + 2n。其中T(n)是一次函数,说明时间的增长趋势是线性的,时间复杂度是线性阶。
我们将线性阶的时间复杂度记为O(n),这个数学符号称为「Big-O Notation」,用来表示函数T(n)的「渐近上界 Asymptotic Upper Bound」。
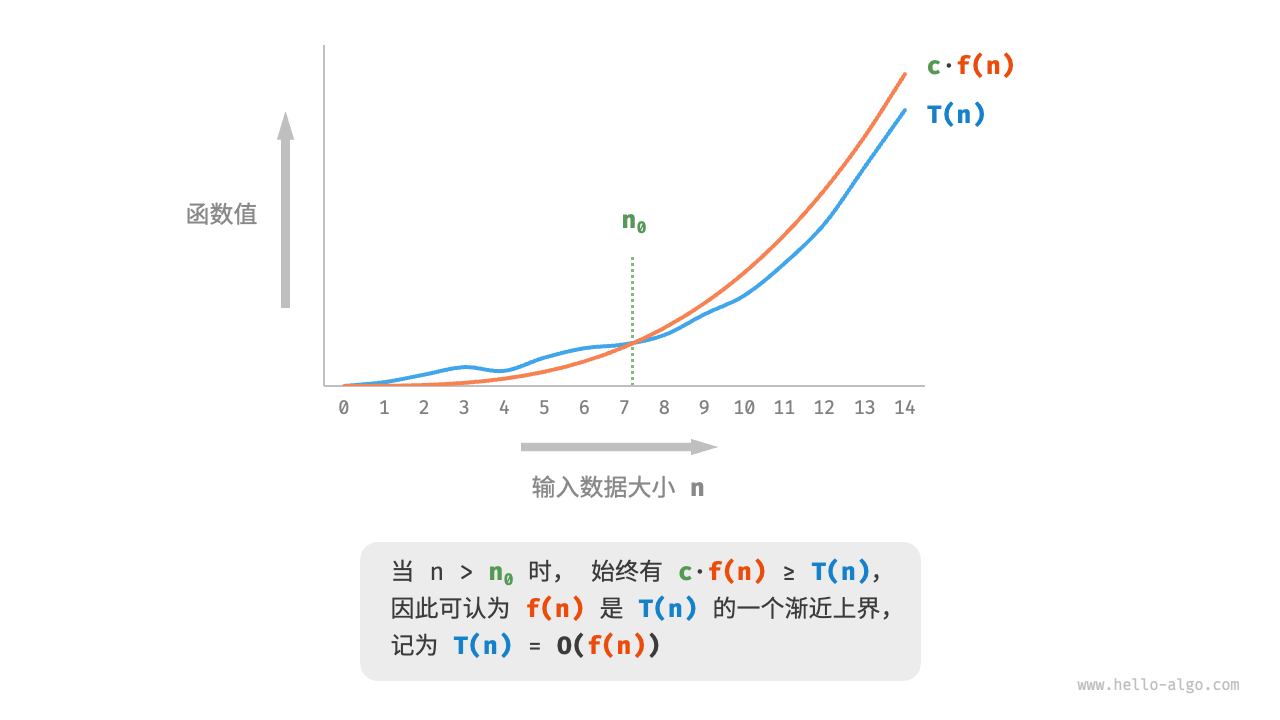
总的来说,计算渐近上界就是寻找一个函数f(n),使得当n趋向于无穷大时,T(n)和f(n)处于相同的增长级别,仅相差一个常数项c的倍数。
推算方法
根据定义,确定f(n)之后,我们便可推算时间复杂度O(f(n))。那么如何确定渐近上界f(n)呢?总体分为两步,统计操作数量,判断渐近上界。
第一步:统计操作数量
针对代码,逐行从上到下计算即可。然而,由于上述c·f(n)中的常数项c可以取任意大小,因此操作数量 T(n)中的各种系数、常数项都可以被忽略。
- 忽略常数项。因为它们都与
n无关,所以对时间复杂度不产生影响。 - 省略所有系数。例如,循环
2n次、5n + 1次等,都可以简化记为n次,因为n前面的系数对时间复杂度没有影响。 - 循环嵌套时使用乘法。总操作数量等于外层循环和内层循环操作数量之积,每一层循环依然可以分别套用上述两个技巧。
void algorithm(int n) { |
下面展示了使用上述技巧前、后的统计结果。两者推出的时间复杂度相同,即为O(n^2)。
T(n) = 2n(n + 1) + (5n + 1) + 2 = 2n^2 + 7n + 3(完整统计)T(n) = n^2 + n(偷懒统计)
第二步:判断渐近上界
时间复杂度由多项式T(n)中最高阶的项来决定。这是因为在n趋于无穷大时,最高阶的项将发挥主导作用,其他项的影响都可以被忽略。
操作数量T(n) |
时间复杂度O(f(n)) |
|---|---|
100000 |
O(1) |
3n + 2 |
O(n) |
2n^2 + 3n + 2 |
O(n^2) |
n^3 + 100000n^2 |
O(n^3) |
2^n + 100000n^100000 |
O(2^n) |
常见类型
设输入数据大小为n,常见的时间复杂度类型包括(按照从低到高的顺序排列)

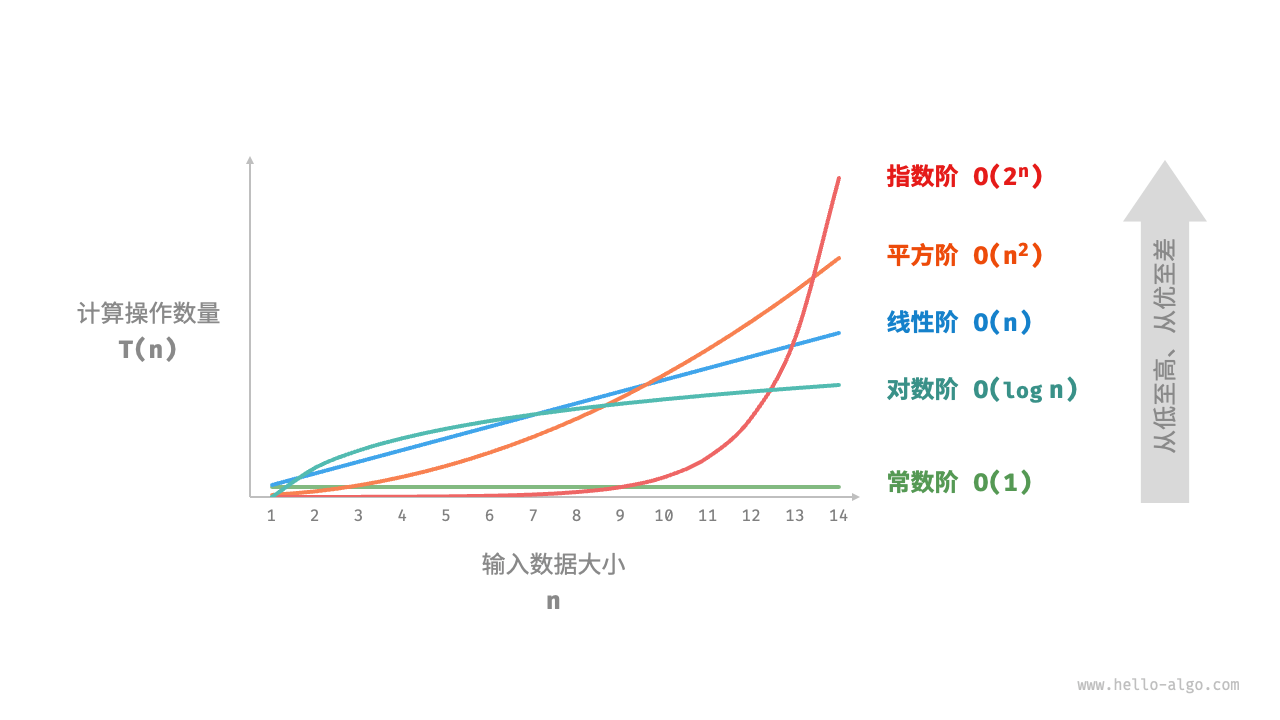
常数阶O(1)
常数阶的操作数量与输入数据大小n无关,不会随着n的变化而变化。
/* 常数阶 */ |
上面代码中,尽管操作数量size很大,但由于其与数据大小n无关,因此时间复杂度仍为O(1)。
线性阶O(n)
线性阶的操作数量相对于输入数据大小以线性级别增长。线性阶通常出现在单层循环中。
/* 线性阶 */ |
遍历数组和遍历链表等操作的时间复杂度均为O(n),其中n为数组或链表的长度。
/* 线性阶(遍历数组) */ |
注意,数据大小n需根据输入数据的类型来具体确定。比如在第一个示例中,变量n为输入数据大小。在第二个示例中,n为数组长度大小。
平方阶O(n^2)
平方阶的操作数量相对于输入数据大小以平方级别增长。平方阶通常出现在嵌套循环中,外层循环和内层循环都为O(n),因此总体为O(n^2)。
/* 平方阶 */ |
以「冒泡排序」为例,外层循环执行n - 1次,内层循环执行n - 1, n - 2, ... , 2, 1次,平均为n / 2次,因此时间复杂度为O(n^2)。
时间复杂度: O((n - 1) · n / 2) = O(n^2)
/* 平方阶(冒泡排序) */ |
指数阶O(2^n)
生物学中的“细胞分裂”是指数阶增长的典型例子。初始状态为1个细胞,分裂一轮后变为2个,分裂两轮后变为4个,以此类推,分裂n轮后有2^n个细胞。
/* 指数阶(循环实现) */ |
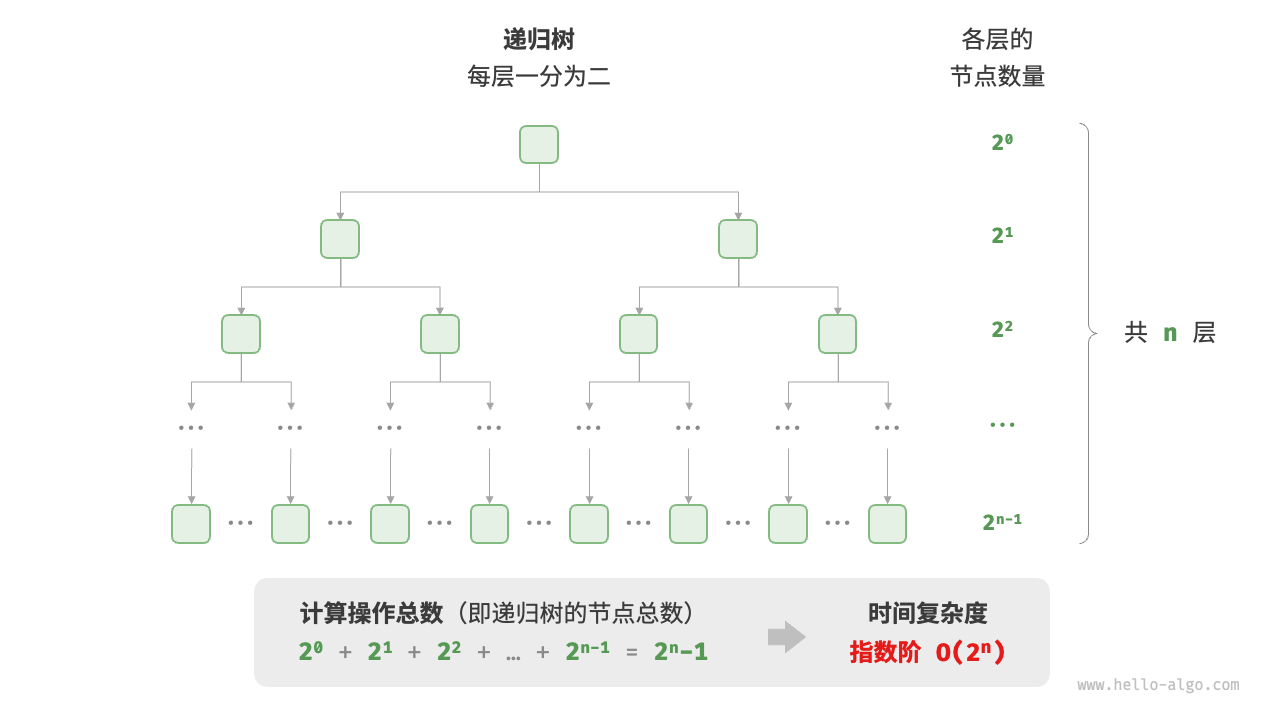
实际算法中,指数阶常出现于递归函数。例如以下代码,其递归地一分为二,经过n次分裂后停止。
/* 指数阶(递归实现) */ |
指数阶增长非常迅速,在穷举法(暴力搜索、回溯等)中比较常见。对于数据规模较大的问题,指数阶是不可接受的,通常需要使用「动态规划」或「贪心」等算法来解决。
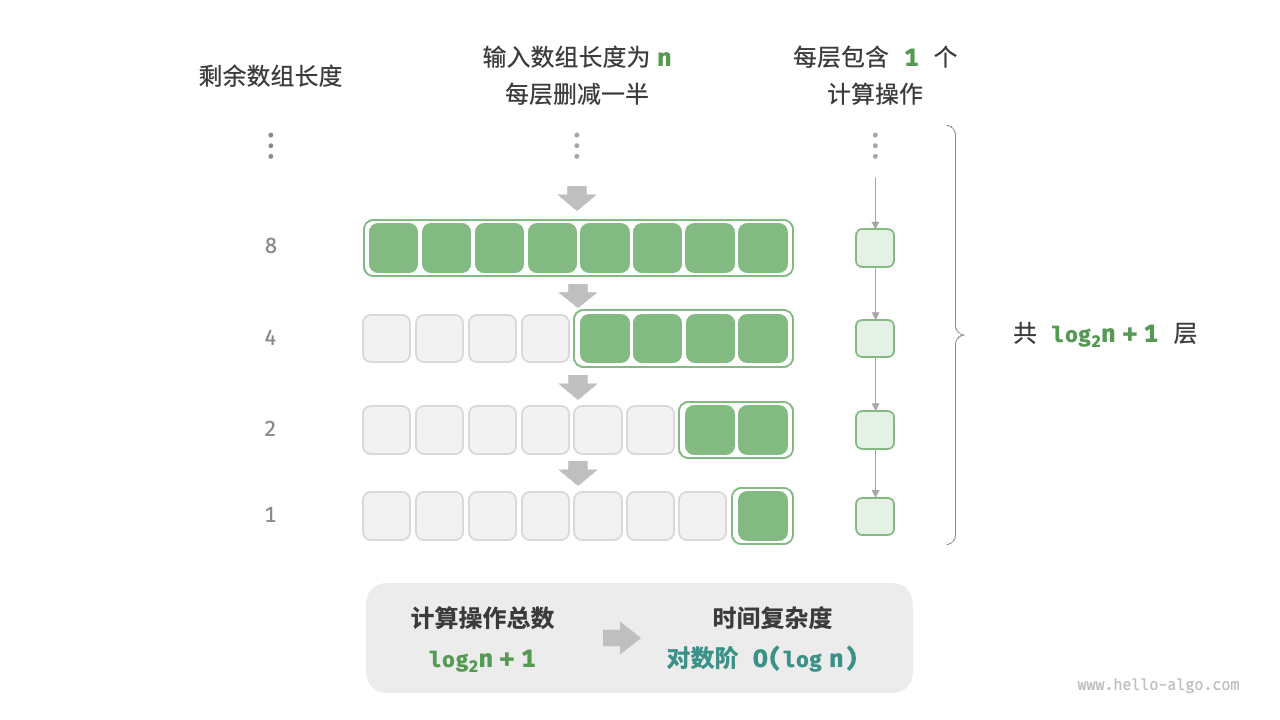
对数阶O(logn)
与指数阶相反,对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为n,由于每轮缩减到一半,因此循环次数是log2(n),即2^n的反函数。
/* 对数阶(循环实现) */ |
与指数阶类似,对数阶也常出现于递归函数。以下代码形成了一个高度为log2(n)的递归树。
/* 对数阶(递归实现) */ |
对数阶常出现于基于「分治」的算法中,体现了“一分为多”和“化繁为简”的算法思想。它增长缓慢,是理想的时间复杂度,仅次于常数阶。
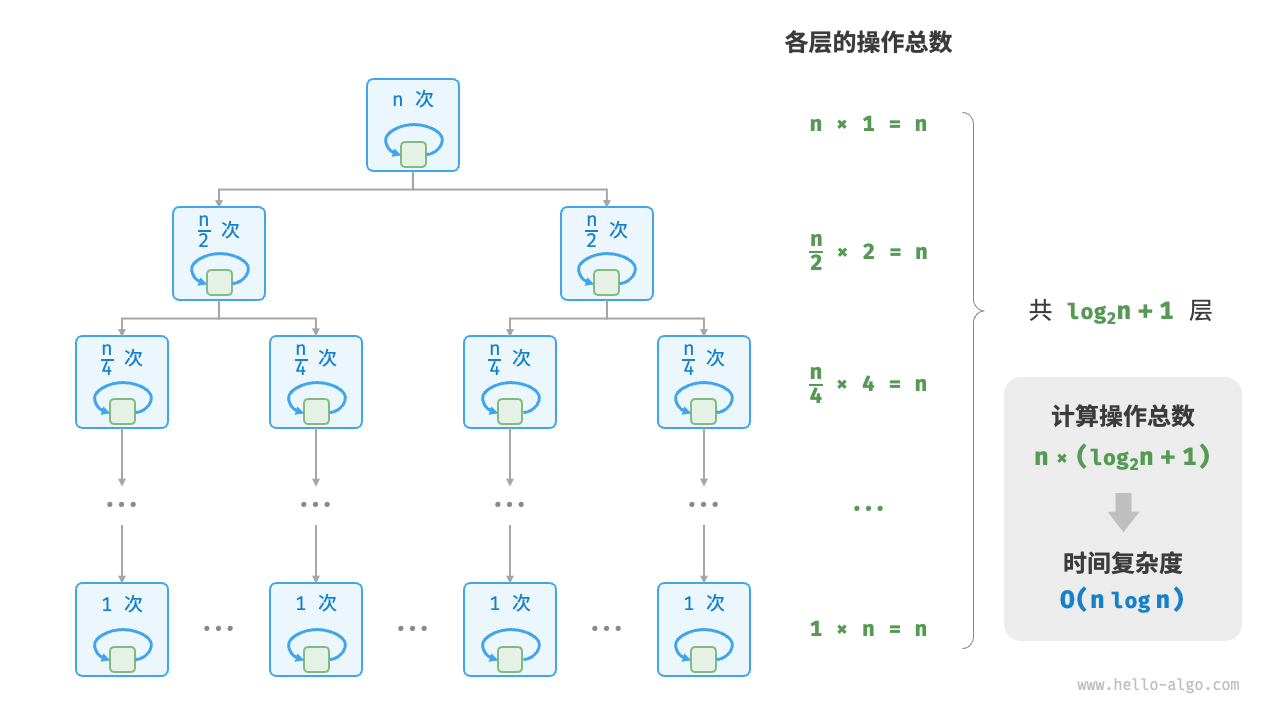
线性对数阶O(nlogn)
线性对数阶常出现于嵌套循环中,两层循环的时间复杂度分别为O(logn)和O(n)。主流排序算法的时间复杂度通常为O(nlogn),例如快速排序、归并排序、堆排序等。
/* 线性对数阶 */ |
阶乘阶O(n!)
阶乘阶对应数学上的“全排列”问题。给定n个互不重复的元素,求其所有可能的排列方案,方案数量为n! = n * (n - 1) * (n - 2) * ... * 2 * 1。
阶乘通常使用递归实现。例如以下代码,第一层分裂出n个,第二层分裂出n-1个,以此类推,直至第n层时终止分裂。
/* 阶乘阶(递归实现) */ |
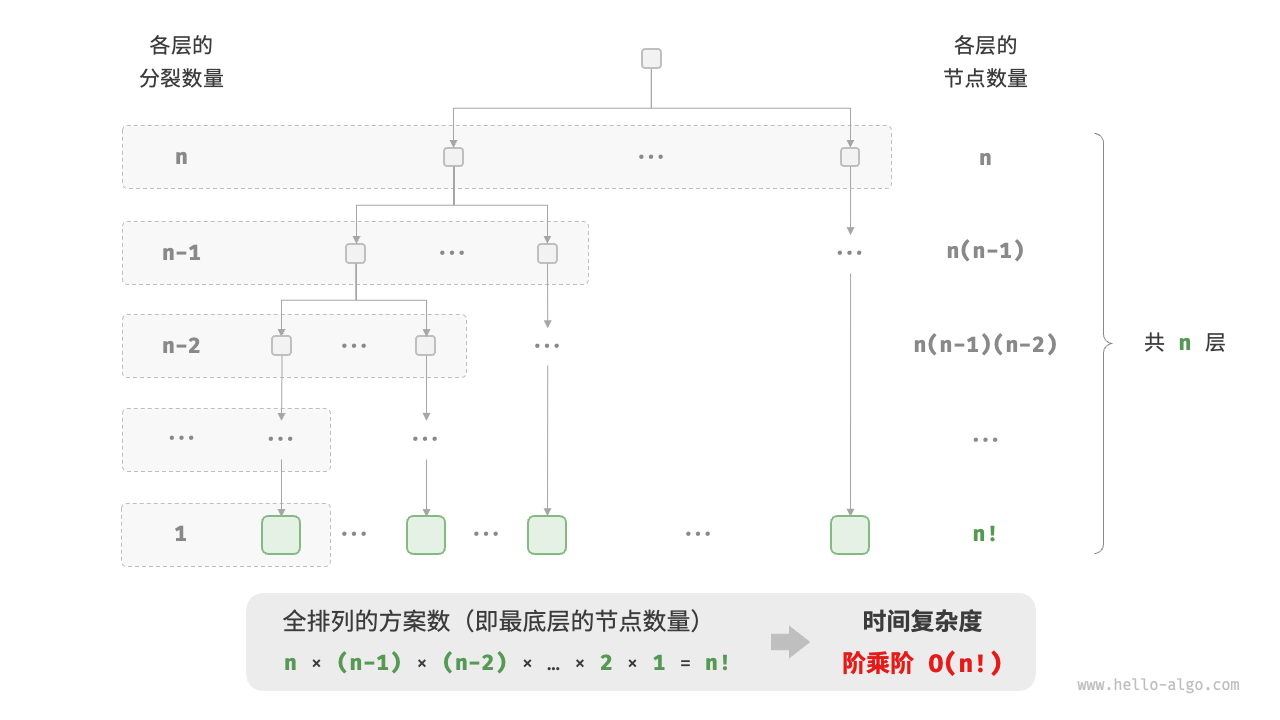
请注意,因为n! > 2^n,所以阶乘阶比指数阶增长地更快,在n较大时也是不可接受的。
最差、最佳、平均
算法的时间效率往往不是固定的,而是与输入数据的分布有关。假设输入一个长度为n的数组nums,其中nums由从1至n的数字组成,但元素顺序是随机打乱的,任务目标是返回元素1的索引。可以得出以下结论。
- 当末尾元素是
1时,需要完整遍历数组,达到最差时间复杂度O(n)。 - 当首个数字为
1时,无论数组多长都不需要继续遍历,达到最佳时间复杂度Ω(1)。
「最差时间复杂度」对应函数渐近上界,使用O记号表示。相应地,「最佳时间复杂度」对应函数渐近下界,用Ω记号表示。
/* 查找数组 nums 中数字 1 所在索引 */ |
然而,实际中很少使用「最佳时间复杂度」,因为通常只有在很小概率下才能达到,并且可能会带来一定的误导性。因此「最差时间复杂度」更为实用,因为它给出了一个效率安全值。
从上面代码可以看出,最差或最佳时间复杂度只出现于“特殊的数据分布”,这些情况的出现概率可能很小。相比之下,「平均时间复杂度」可以体现算法在随机输入数据下的运行效率,用Θ记号来表示。
- 上面代码中,输入数组是被打乱的,元素
1出现在任意索引的概率都是相等的,那么算法的平均循环次数则是数组长度的一半n / 2,平均时间复杂度为Θ(n / 2) = Θ(n)。
值得说明的是,由于计算平均时间复杂度往往比较困难,因为很难分析出在数据分布下的整体数学期望。所以,我们通常使用最差时间复杂度作为算法效率的评判标准。
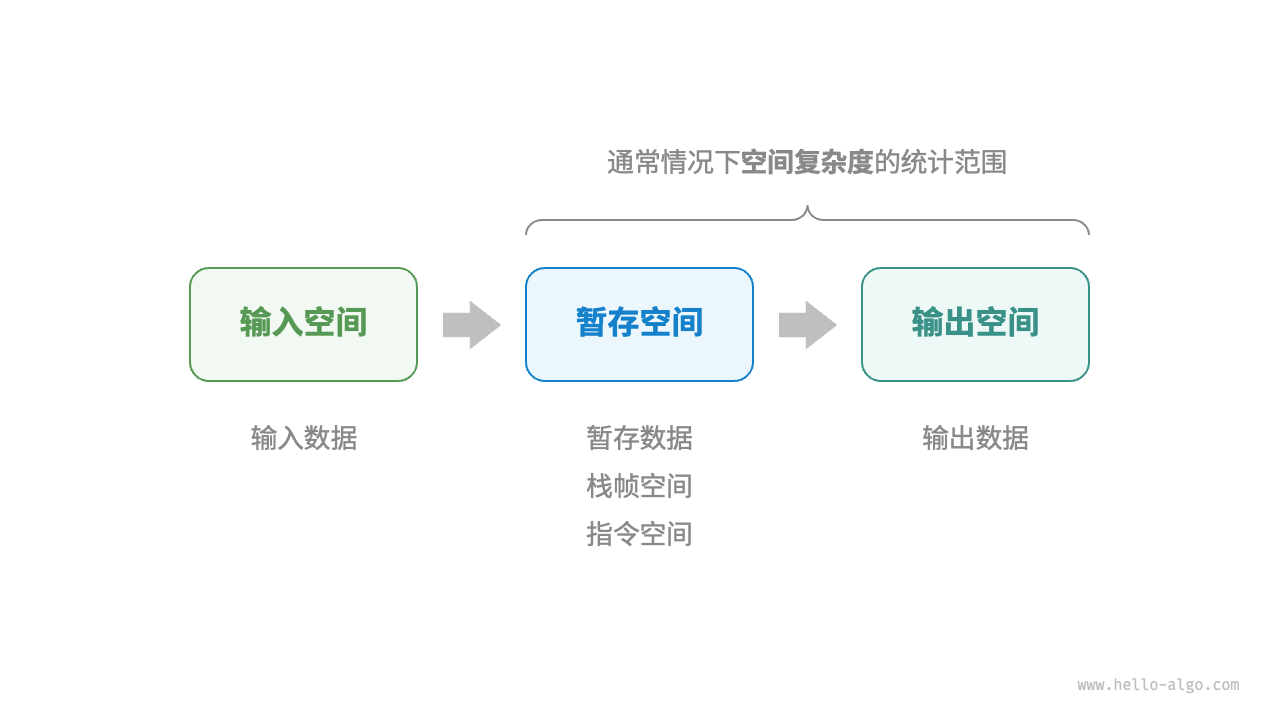
2.3 空间复杂度
「空间复杂度」用于衡量算法占用内存空间随着数据量变大时的增长趋势。这个概念与时间复杂度非常类似,只需将“运行时间”替换为“占用内存空间”。
推算方法
空间复杂度的推算方法与时间复杂度大致相同,只需将统计对象从“操作数量”转为“使用空间大小”。
而与时间复杂度不同的是,通常只关注最差空间复杂度。因为内存空间是一项硬性要求,必须确保在所有输入数据下都有足够的内存空间预留。
下面代码中,最差空间复杂度中的“最差”有两层含义。
void algorithm(int n) { |
- 以最差输入数据为准。当
n < 10时,空间复杂度为O(1)。当n > 10时,初始化的数组nums占用O(n)空间,因此最差空间复杂度为O(n)。 - 以算法运行中的峰值内存为准。程序在执行最后一行之前,占用
O(1)空间。当初始化数组nums时,程序占用O(n)空间;因此最差空间复杂度为O(n)。
在递归函数中,则需要注意统计栈帧空间。
int function() { |
- 函数
loop()在循环中调用了n次function(),每轮中function()都返回并释放了栈帧空间,因此空间复杂度仍为O(1)。 - 递归函数
recur()在运行过程中会同时存在n个未返回的recur(),从而占用O(n)的栈帧空间。
常见类型
设输入数据大小为n,下图展示了常见的空间复杂度类型(从低到高排列)。

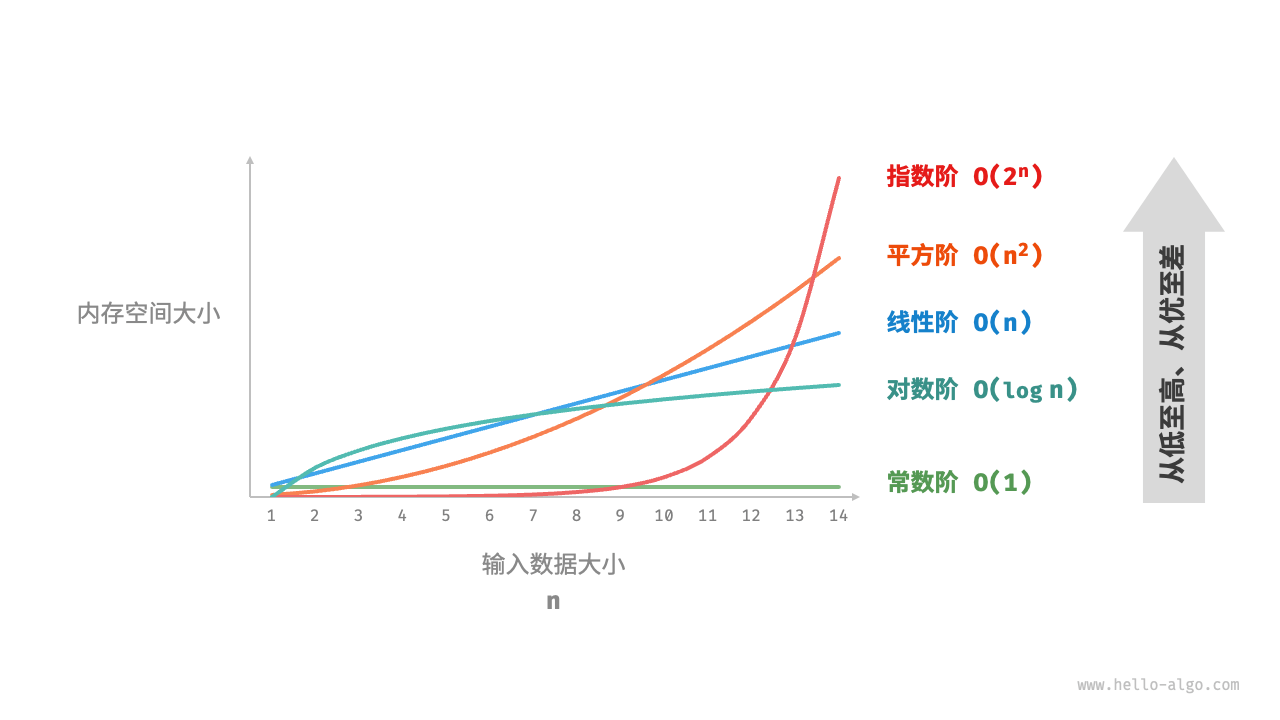
常数阶O(1)
常数阶常见于数量与输入数据大小n无关的常量、变量、对象。
注意,在循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,因此不会累积占用空间,空间复杂度仍为O(1)。
/* 函数 */ |
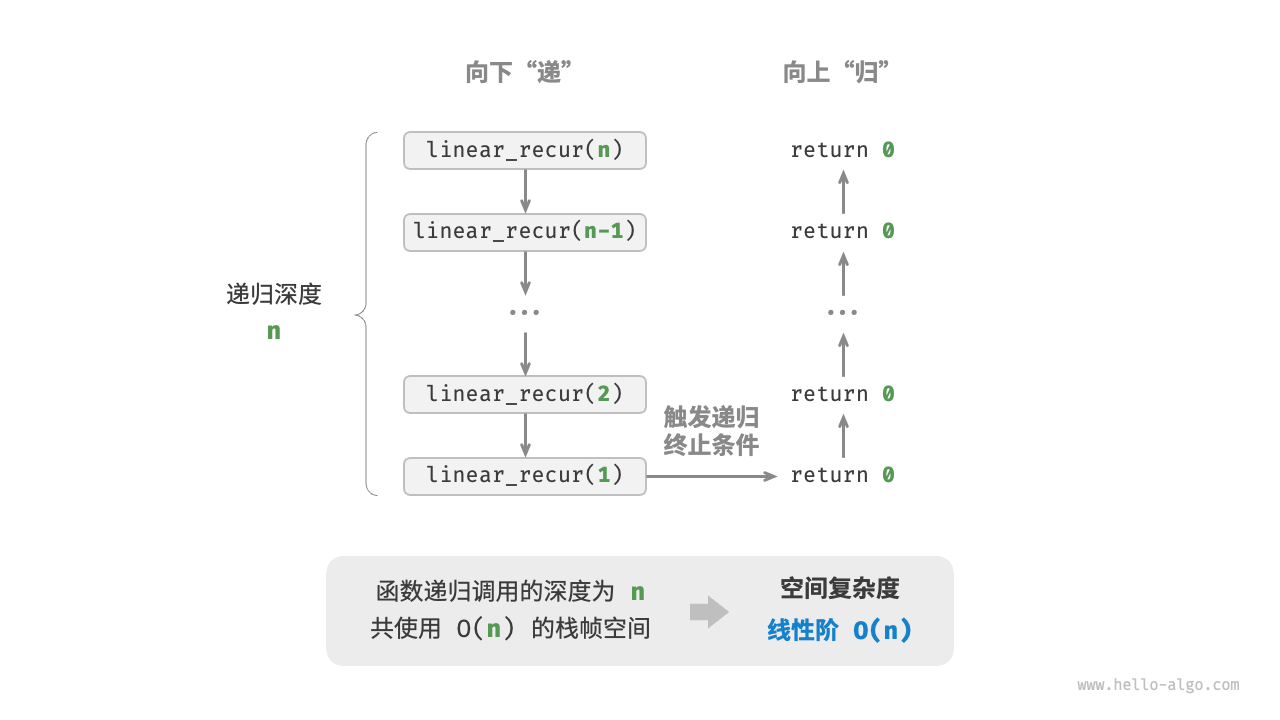
线性阶O(n)
线性阶常见于元素数量与n成正比的数组、链表、栈、队列等。
/* 线性阶 */ |
如下图所示,下面代码的递归深度为n,即同时存在n个未返回的linear_recur()函数,使用O(n)大小的栈帧空间。
/* 线性阶(递归实现) */ |
平方阶O(n^2)
平方阶常见于矩阵和图,元素数量与n成平方关系。
/* 平方阶 */ |
如下图所示,下面代码的递归深度为n,每个递归函数中都初始化了一个数组,长度分别为n, n - 1, n - 2, ..., 2, 1,平均长度为n / 2,因此总体占用O(n^2)空间。
/* 平方阶(递归实现) */ |

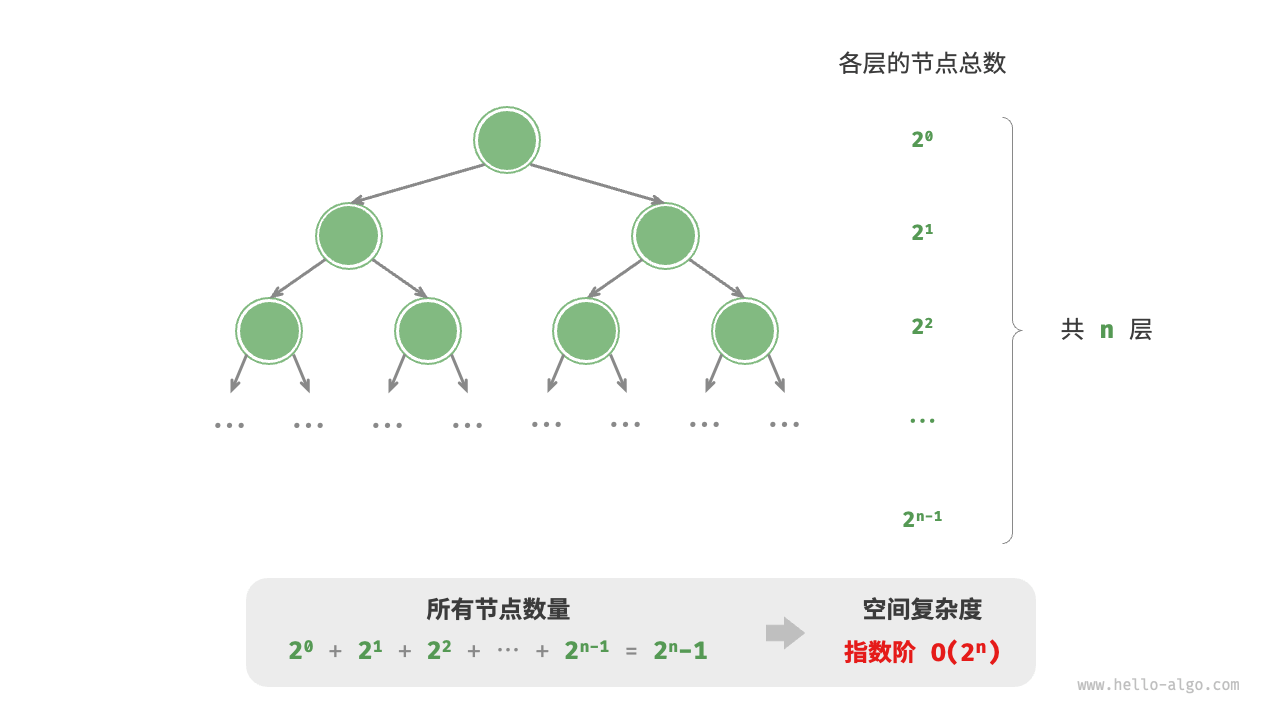
指数阶O(2^n)
指数阶常见于二叉树。下图,高度为n的“满二叉树”的节点数量为2^n - 1,占用O(2^n)空间。
/* 指数阶(建立满二叉树) */ |
对数阶O(logn)
对数阶常见于分治算法。例如归并排序,输入长度为n的数组,每轮递归将数组从中点划分为两半,形成高度为logn的递归树,使用O(logn)栈帧空间。
权衡时间与空间
理想情况下,我们希望算法的时间复杂度和空间复杂度都能达到最优。然而在实际情况中,同时优化时间复杂度和空间复杂度通常是非常困难的。
降低时间复杂度通常需要以提升空间复杂度为代价,反之亦然。在大多数情况下,时间比空间更宝贵,因此“以空间换时间”通常是更常用的策略。当然,在数据量很大的情况下,控制空间复杂度也是非常重要的。
3. 数据结构
常见的数据结构包括数组(Array)、链表(List)、栈(Stack)、队列(Queue)、哈希表(Hash Table)、树(Tree)、堆(Heap)、图(Graph),它们可以从“逻辑结构”和“物理结构”两个维度进行分类。
3.1 数据结构分类
逻辑结构揭示了数据元素之间的逻辑关系。在数组和链表中,数据按照顺序依次排列,体现了数据之间的线性关系。而在树中,数据从顶部向下按层次排列,表现出祖先与后代之间的派生关系。图则由节点和边构成,反映了复杂的网络关系。
如下图所示,逻辑结构可被分为“线性”和“非线性”两大类。线性结构比较直观,指数据在逻辑关系上呈线性排列。非线性结构则相反,呈非线性排列。
- 线性数据结构:数组、链表、栈、队列、哈希表。
- 非线性数据结构:树、堆、图、哈希表。
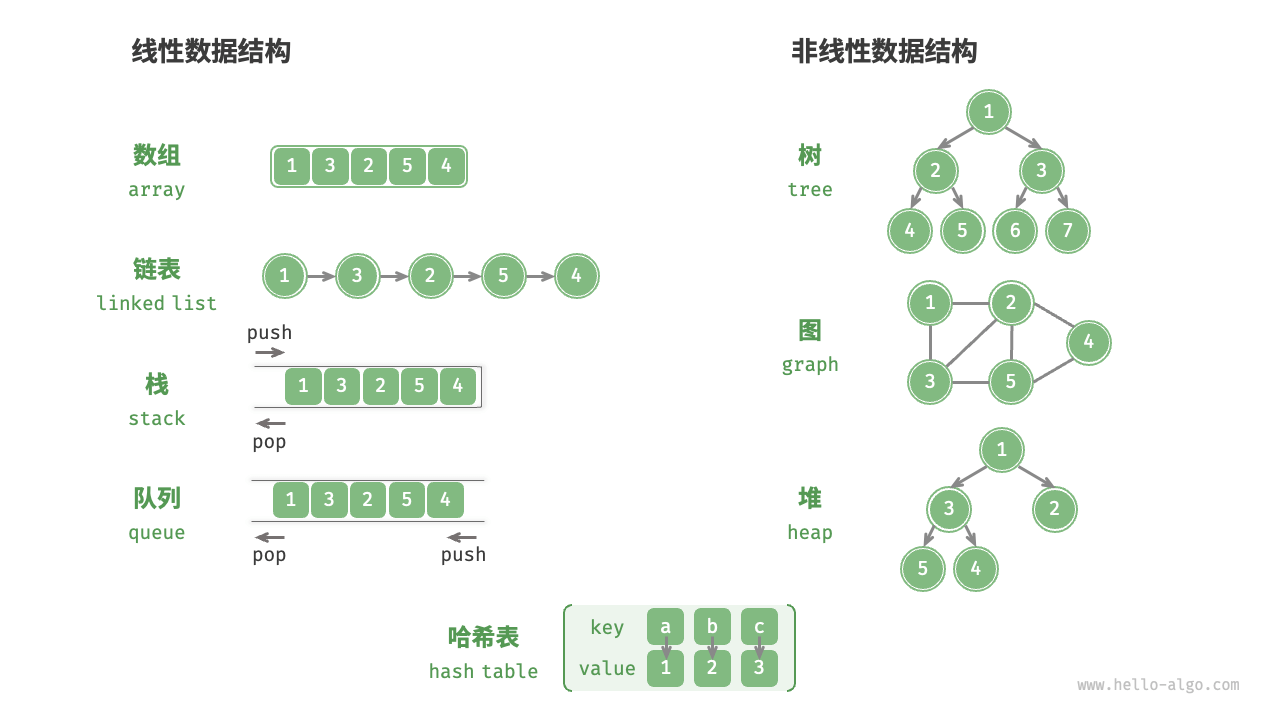
非线性数据结构可以进一步被划分为树形结构和网状结构。
- 线性结构:数组、链表、队列、栈、哈希表,元素之间是一对一的顺序关系。
- 树形结构:树、堆、哈希表,元素之间是一对多的关系。
- 网状结构:图,元素之间是多对多的关系。
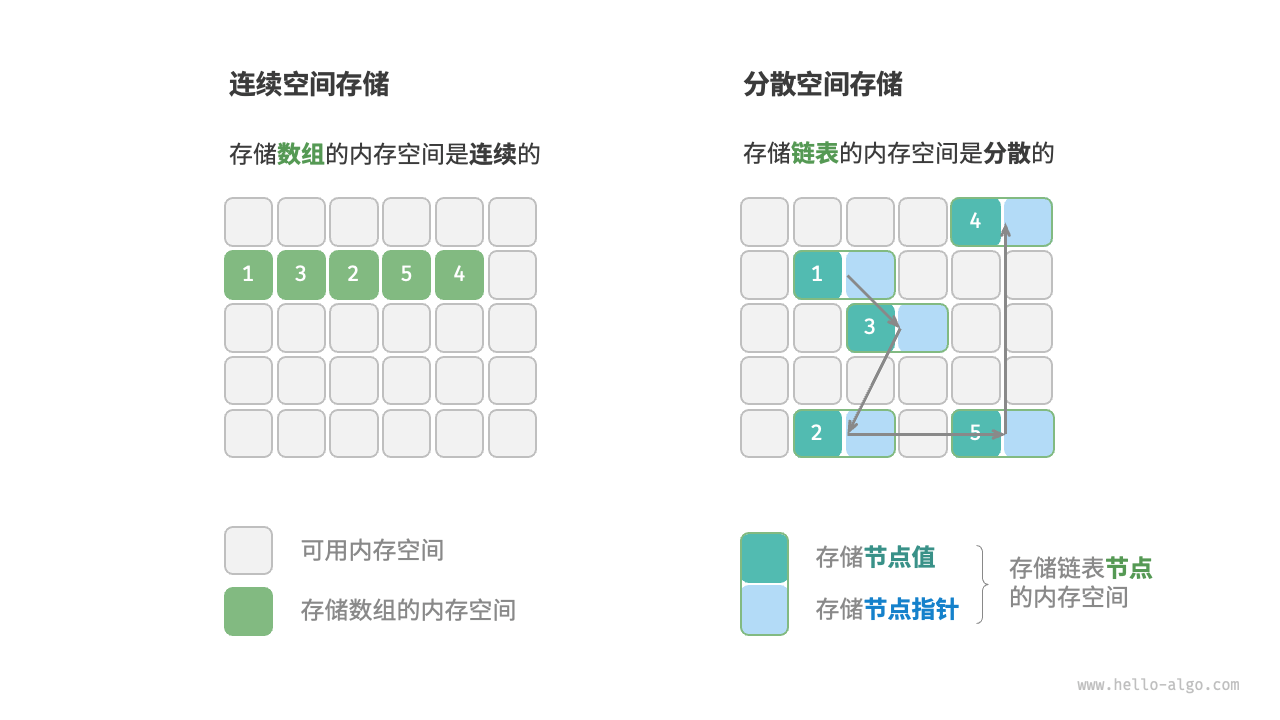
物理结构反映了数据在计算机内存中的存储方式。在算法运行过程中,数据都存储在内存中,系统通过内存地址来访问目标位置的数据。如下图所示,存储方式可分为连续空间存储和离散空间存储。
3.2 基本数据类型
基本数据类型是CPU可以直接进行运算的类型,在算法中直接被使用。
- 整数类型
byte,short,int,long。 - 浮点数类型
float,double,用于表示小数。 - 字符类型
char,用于表示各种语言的字母、标点符号、甚至表情符号等。 - 布尔类型
bool,用于表示“是”与“否”判断。
基本数据类型以二进制的形式存储在计算机中。一个二进制位即为1比特。在绝大多数现代系统中,1字节(byte)由8比特(bits)组成。

4. 数组与链表
4.1 数组
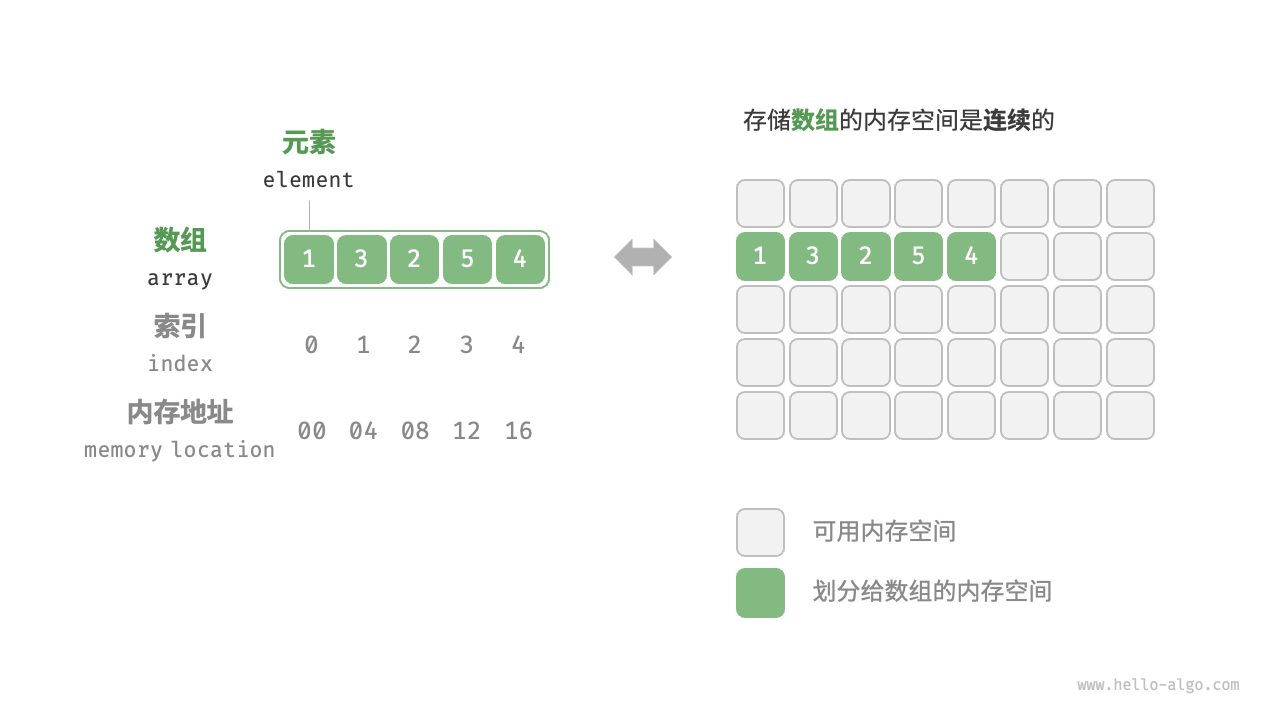
「数组 array」是一种线性数据结构,其将相同类型元素存储在连续的内存空间中。而元素在数组中的位置称为该元素的「索引 index」。
数组常用操作
(1)初始化数组
可以根据需求选用数组的两种初始化方式,无初始值、给定初始值。在未指定初始值的情况下,大多数编程语言会将数组元素初始化为0。
array.java |
(2)访问元素
数组元素被存储在连续的内存空间中,这意味着计算数组元素的内存地址非常容易。给定数组内存地址(即首元素内存地址)和某个元素的索引,可以使用以下公式计算得到该元素的内存地址,从而直接访问此元素。
# 元素内存地址 = 数组内存地址 + 元素长度 * 元素索引 |
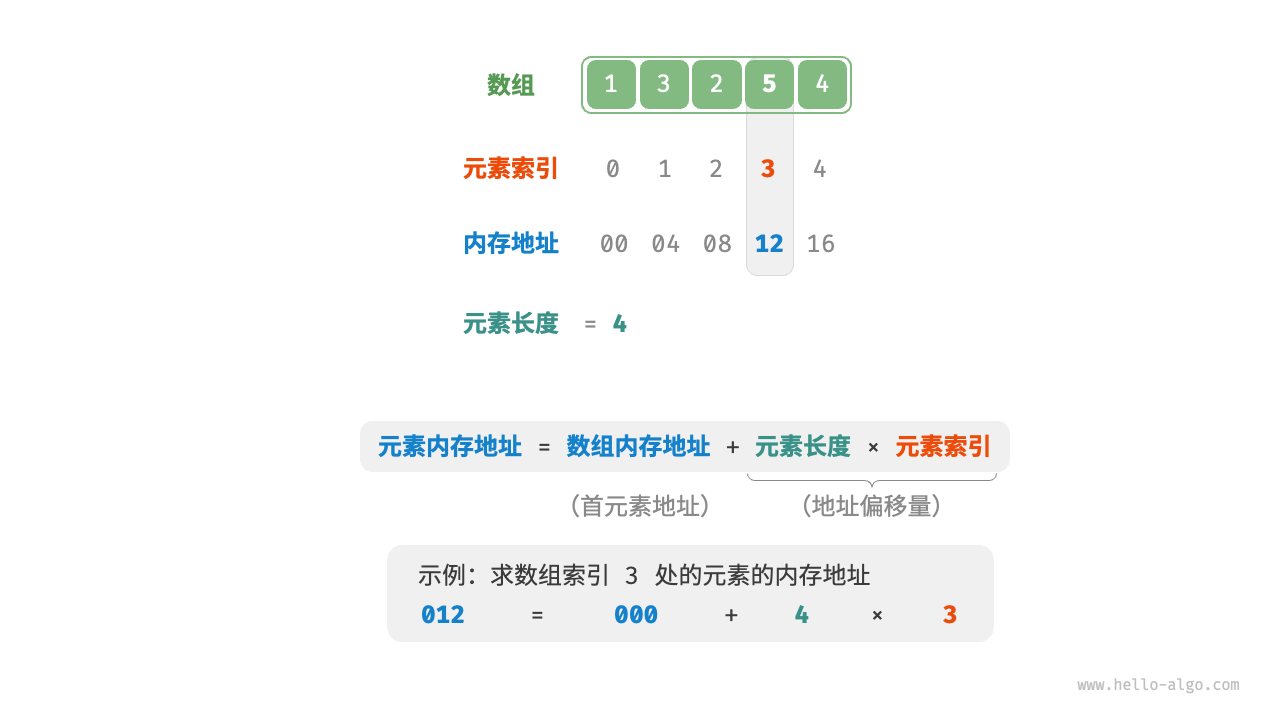
在数组中访问元素是非常高效的,我们可以在O(1)时间内随机访问数组中的任意一个元素。
/* 随机访问元素 */ |
(3)插入元素
数组元素在内存中是“紧挨着的”,它们之间没有空间再存放任何数据。如下图所示,如果想要在数组中间插入一个元素,则需要将该元素之后的所有元素都向后移动一位,之后再把元素赋值给该索引。
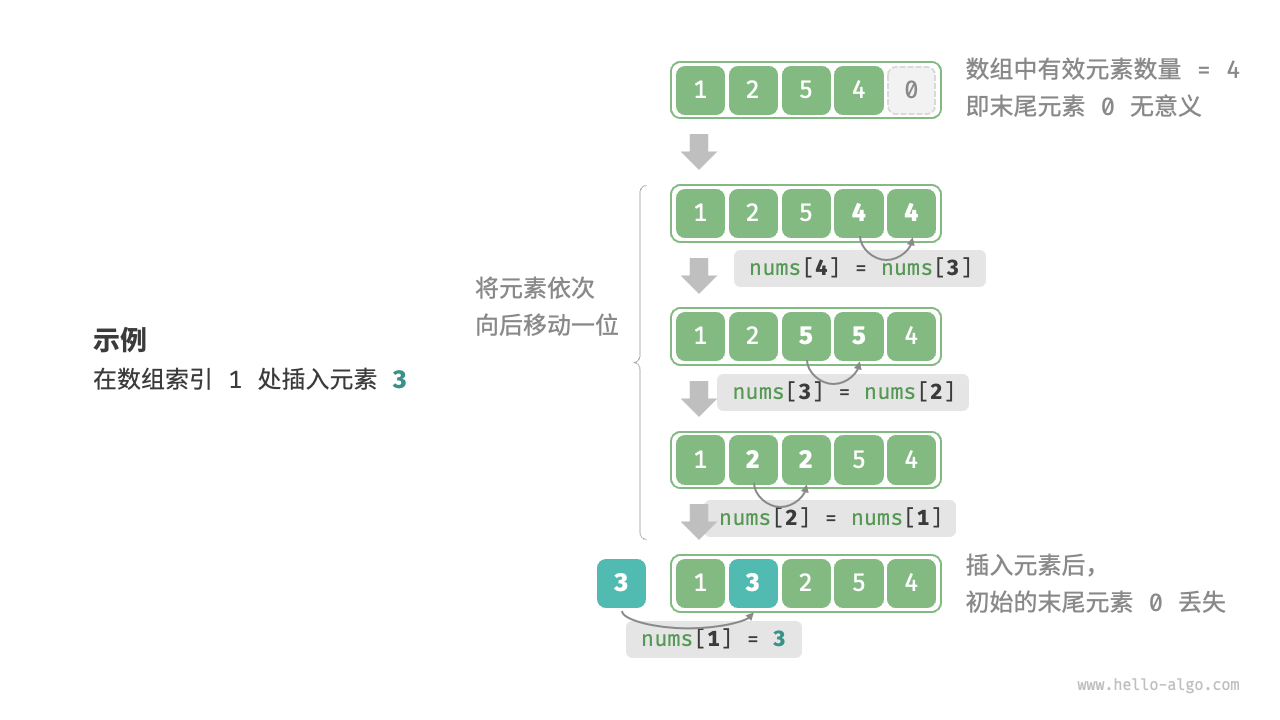
注意,由于数组的长度是固定的,因此插入一个元素必定会导致数组尾部元素的“丢失”。
/* 在数组的索引 index 处插入元素 num */ |
(4)删除元素
同理,如下图所示,若想要删除索引i处的元素,则需要把索引i之后的元素都向前移动一位。
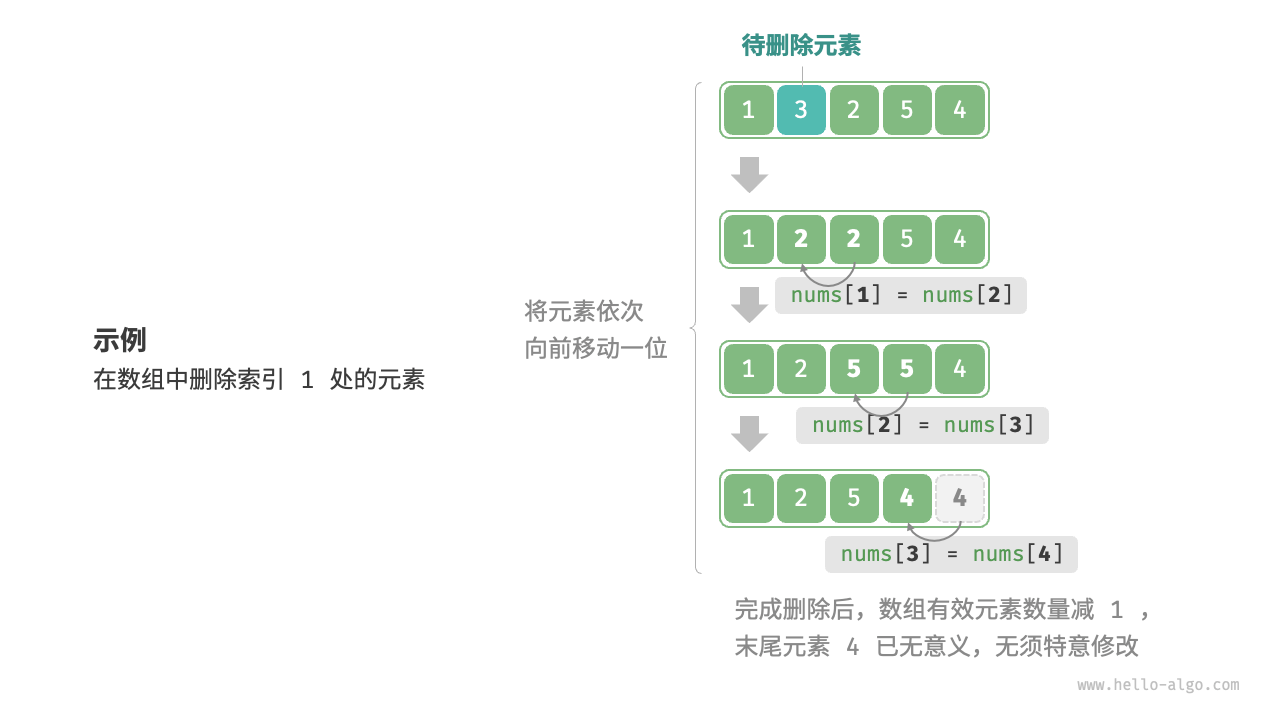
注意,删除元素完成后,原先末尾的元素变得“无意义”了,所以我们无须特意去修改它。
/* 删除索引 index 处元素 */ |
总的来看,数组的插入与删除操作有以下缺点。
- 时间复杂度高:数组的插入和删除的平均时间复杂度均为
O(n),其中n为数组长度。 - 丢失元素:由于数组的长度不可变,因此在插入元素后,超出数组长度范围的元素会丢失。
- 内存浪费:我们可以初始化一个比较长的数组,只用前面一部分,这样在插入数据时,丢失的末尾元素都是“无意义”的,但这样做也会造成部分内存空间的浪费。
(5)遍历数组
大多数编程语言中,我们既可以通过索引遍历数组,也可以直接遍历获取数组中的每个元素。
/* 遍历数组 */ |
(6)查找元素
在数组中查找指定元素需要遍历数组,每轮判断元素值是否匹配,若匹配则输出对应索引。因为数组是线性数据结构,所以上述查找操作被称为“线性查找”。
/* 在数组中查找指定元素 */ |
(7)扩容数组
大多数编程语言中,数组的长度是不可变的。如果希望扩容数组,则需重新建立一个更大的数组,然后把原数组元素依次拷贝到新数组。这是一个O(n)的操作,在数组很大的情况下是非常耗时。
/* 扩展数组长度 */ |
4.2 链表
「链表 linked list」是一种线性数据结构,其中的每个元素都是一个节点对象,各个节点通过“引用”相连接。引用记录了下一个节点的内存地址,通过它可以从当前节点访问到下一个节点。
链表的设计使得各个节点可以被分散存储在内存各处,它们的内存地址是无须连续的。链表的组成单位是「节点 node」对象。每个节点都包含两项数据,节点的“值”和指向下一节点的“引用”。
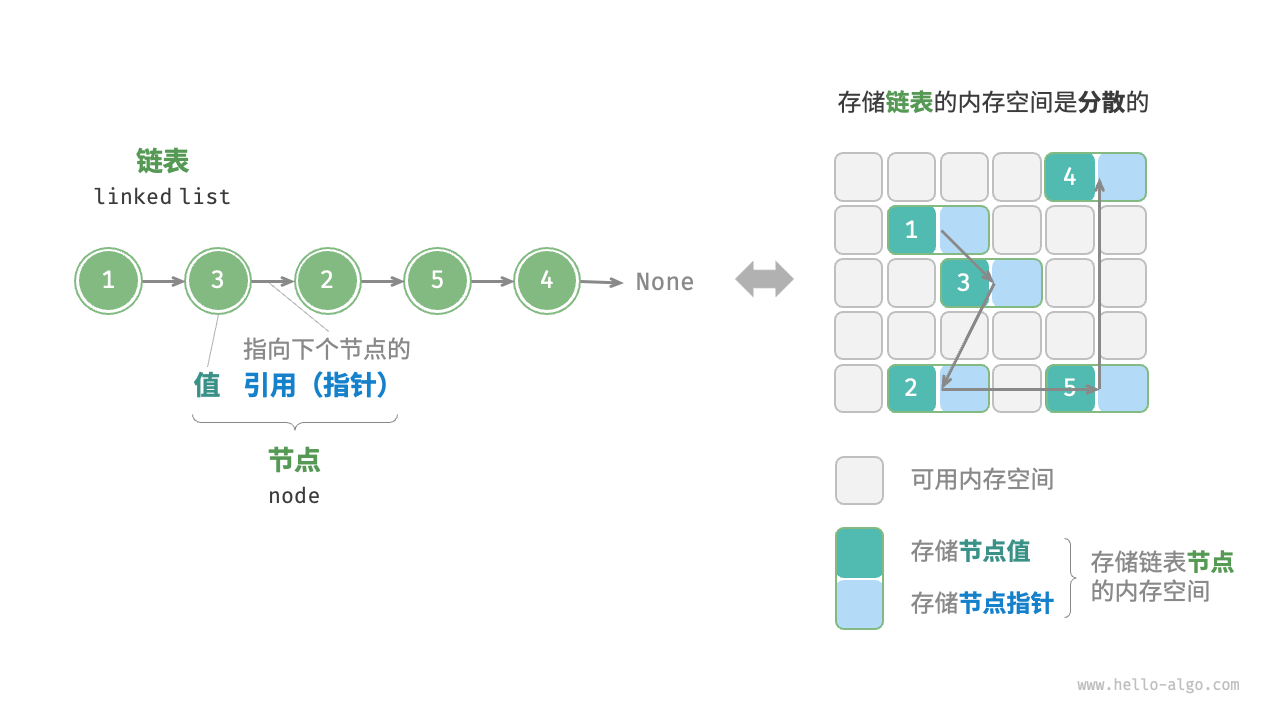
链表常用操作
(1)初始化链表
建立链表分为两步,第一步是初始化各个节点对象,第二步是构建引用指向关系。初始化完成后,就可以从链表的头节点出发,通过引用指向next依次访问所有节点。
/* 初始化链表 1 -> 3 -> 2 -> 5 -> 4 */ |
数组整体是一个变量,比如数组nums包含元素nums[0],nums[1]等,而链表是由多个独立的节点对象组成的。我们通常将头节点当作链表的代称,比如以上代码中的链表可被记做链表n0。
(2)插入节点
在链表中插入节点非常容易。如下图所示,假设我们想在相邻的两个节点n0,n1之间插入一个新节点P,则只需要改变两个节点引用(指针)即可,时间复杂度为O(1)。
相比之下,在数组中插入元素的时间复杂度为O(n),在大数据量下的效率较低。
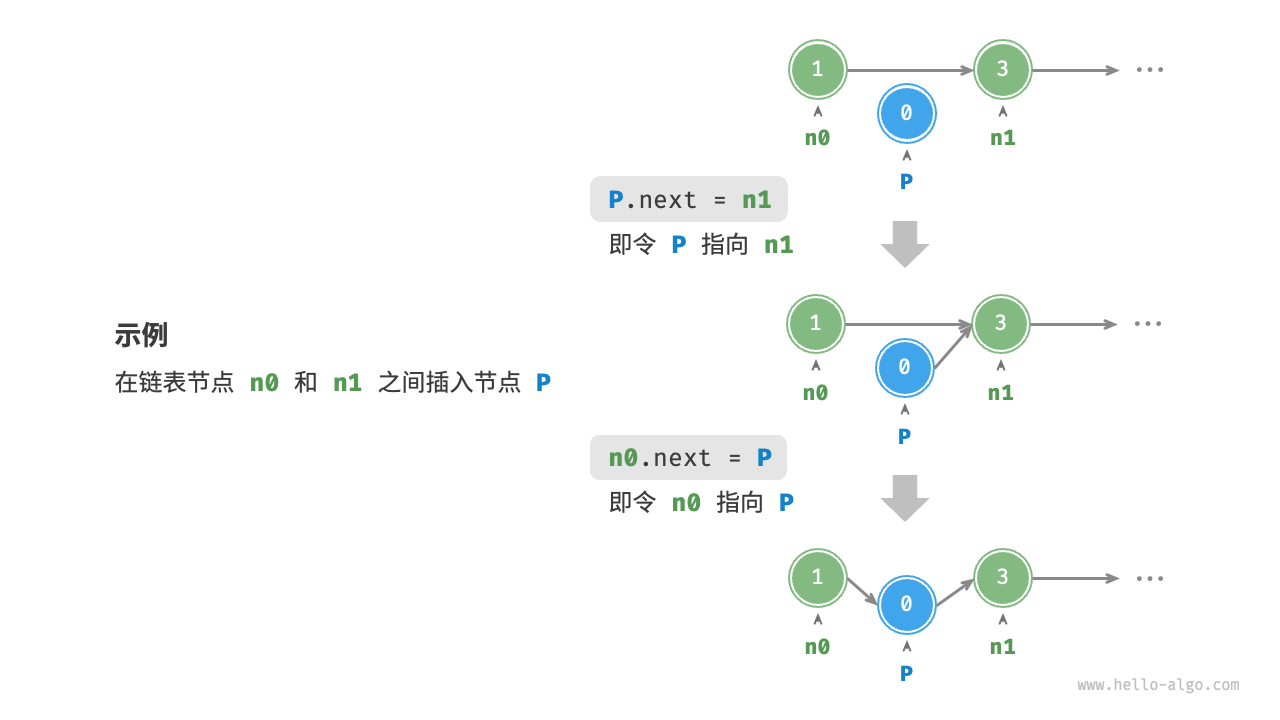
/* 在链表的节点 n0 之后插入节点 P */ |
(3)删除节点
如下图所示,在链表中删除节点也非常方便,只需改变一个节点的引用(指针)即可。
虽然在删除操作完成后节点P仍然指向n1,但实际上遍历此链表已经无法访问到P,这意味着P已经不再属于该链表了。
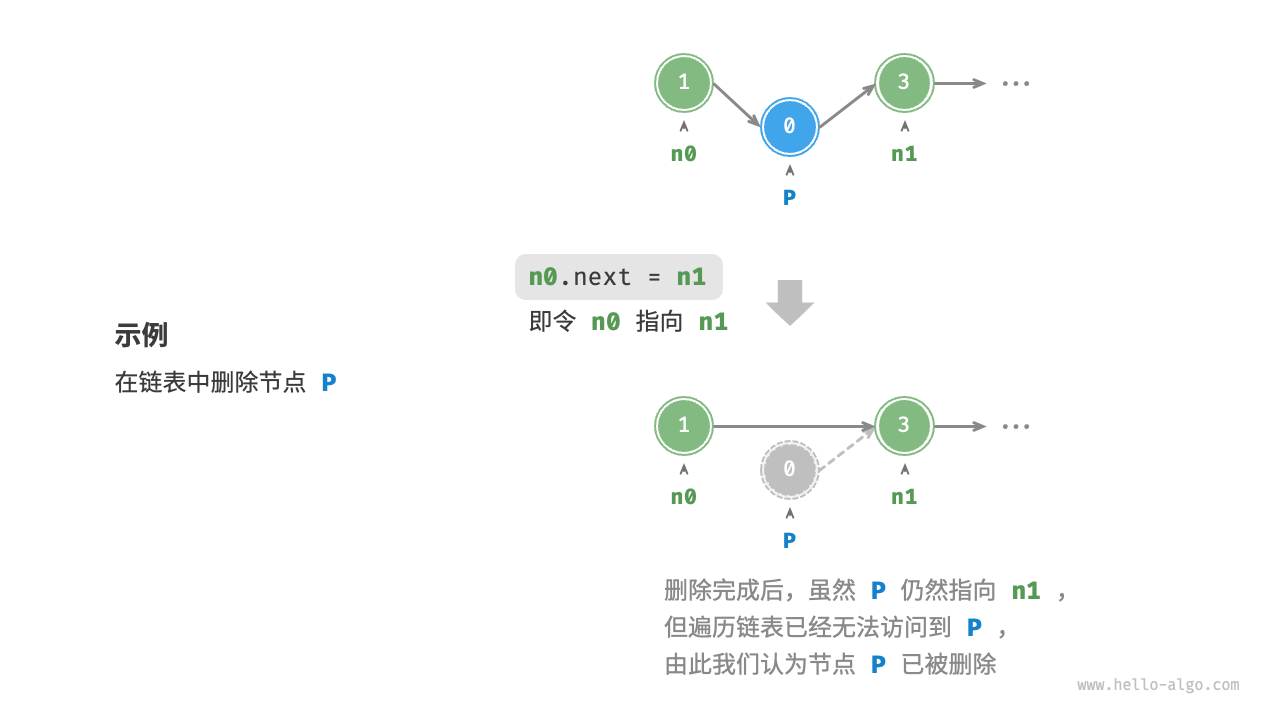
/* 删除链表的节点 n0 之后的首个节点 */ |
(4)访问节点
链表访问节点的效率较低。可以在O(1)时间下访问数组中的任意元素,链表则不行。程序需要从头节点出发,逐个向后遍历,直至找到目标节点。访问链表的第n个节点需要循环n - 1轮,时间复杂度为O(n)。
/* 访问链表中索引为 index 的节点 */ |
(5)查找节点
遍历链表,查找链表内值为target的节点,输出节点在链表中的索引。此过程也属于线性查找。
/* 在链表中查找值为 target 的首个节点 */ |
数组 VS 链表
下面是数组和链表的各项特点与操作效率。由于它们采用两种相反的存储策略,因此各种性质和操作效率也呈现对立的特点。
| 数组 | 链表 | |
|---|---|---|
| 存储方式 | 连续内存空间 | 离散内存空间 |
| 缓存局部性 | 友好 | 不友好 |
| 容量扩展 | 长度不可变 | 可灵活扩展 |
| 内存效率 | 占用内存少、浪费部分空间 | 占用内存多 |
| 访问元素 | O(1) |
O(n) |
| 添加元素 | O(n) |
O(1) |
| 删除元素 | O(n) |
O(1) |
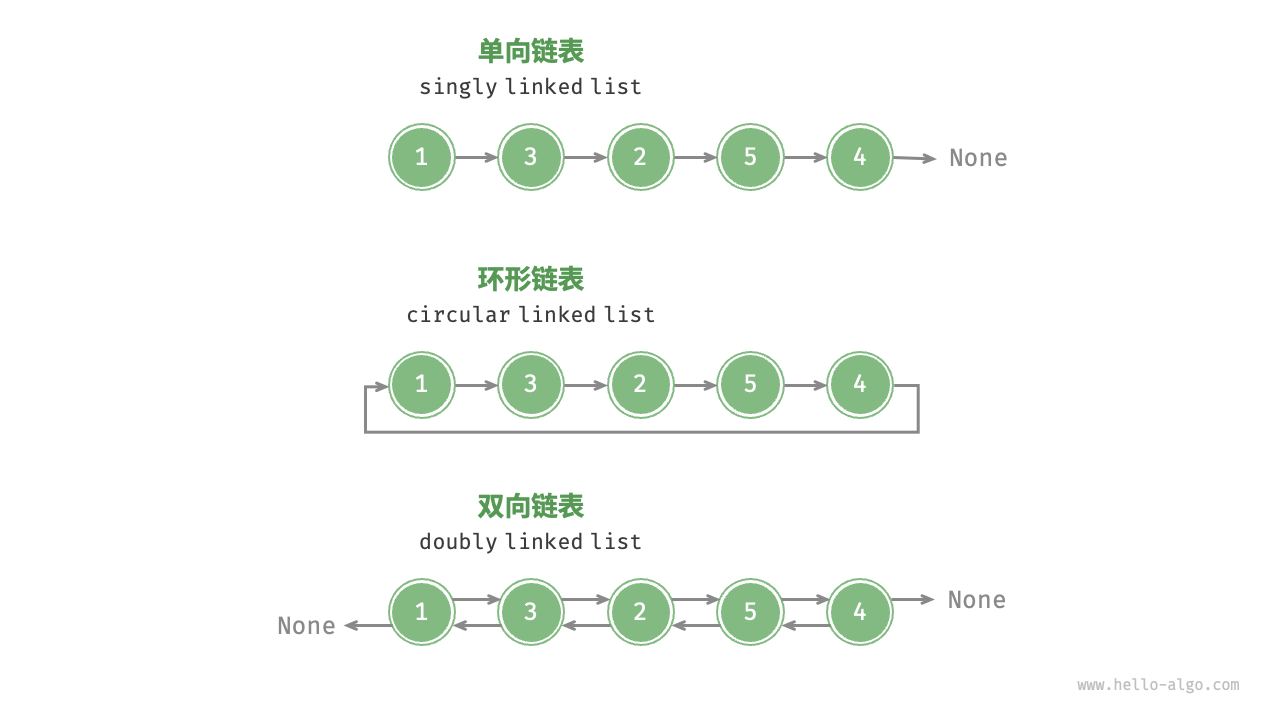
常见链表类型
- 单向链表:即普通链表。单向链表的节点包含值和指向下一节点的引用两项数据。我们将首个节点称为头节点,将最后一个节点成为尾节点,尾节点指向空
Node。 - 环形链表:如果我们令单向链表的尾节点指向头节点(即首尾相接),则得到一个环形链表。在环形链表中,任意节点都可以视作头节点。
- 双向链表:与单向链表相比,双向链表记录了两个方向的引用。双向链表的节点定义同时包含指向后继节点(下一个节点)和前驱节点(上一个节点)的引用(指针)。相较于单向链表,双向链表更具灵活性,可以朝两个方向遍历链表,但相应地也需要占用更多的内存空间。
/* 双向链表节点类 */ |
4.3 列表
「动态数组 dynamic array」是长度可变的数组,也常被称为「列表 list」。它基于数组实现,继承了数组的优点,并且可以在程序运行过程中动态扩容。可以在列表中自由地添加元素,而无须担心超过容量限制。
列表常用操作
(1)初始化列表
可以使用“无初始值”和“有初始值”这两种初始化方法。
/* 初始化列表 */ |
(2)访问元素
列表本质上是数组,因此可以在O(1)时间内访问和更新元素,效率很高。
/* 访问元素 */ |
(3)插入与删除元素
相较于数组,列表可以自由地添加与删除元素。在列表尾部添加元素的时间复杂度为O(1),但插入和删除元素的效率仍与数组相同,时间复杂度为O(n)。
/* 清空列表 */ |
(4)遍历列表
与数组一样,列表可以根据索引遍历,也可以直接遍历各元素。
/* 通过索引遍历列表 */ |
(5)拼接列表
给定一个新列表list1,我们可以将该列表拼接到原列表的尾部。
/* 拼接两个列表 */ |
(6)排序列表
完成列表排序后,便可以使用在数组类算法题中经常考察的“二分查找”和“双指针”算法。
/* 排序列表 */ |
5. 栈与队列
5.1 栈
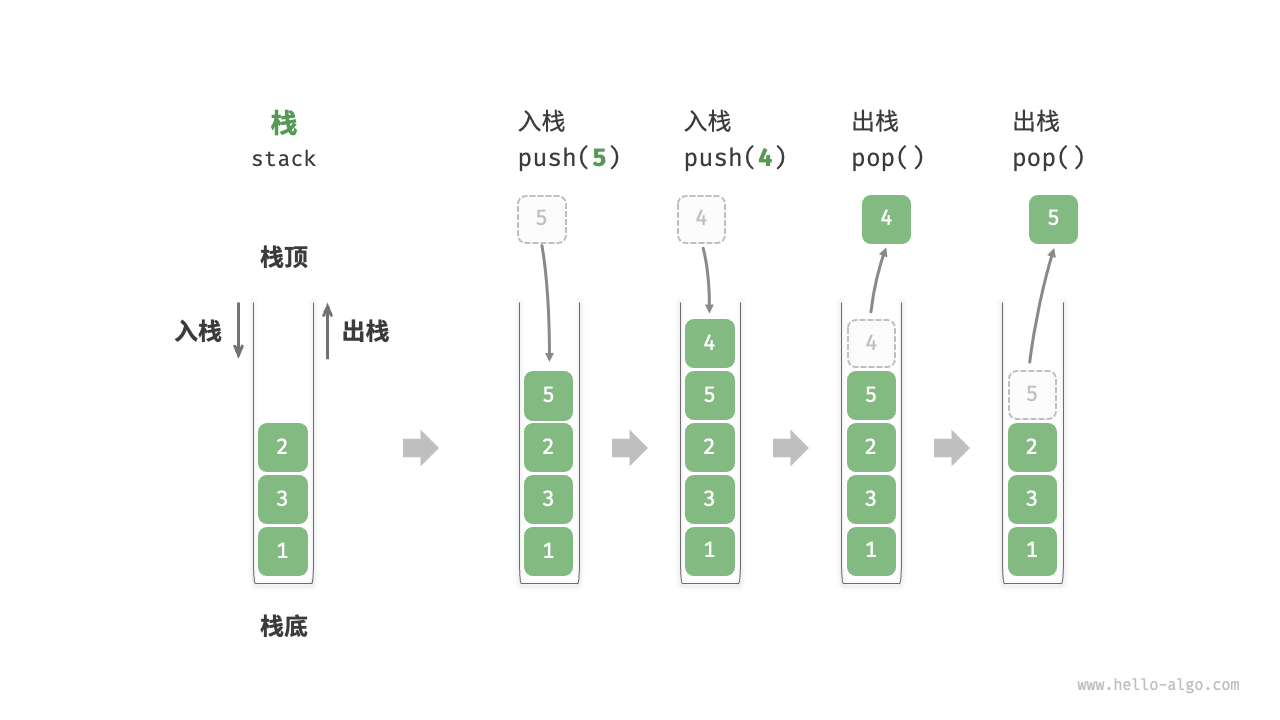
「栈 stack」是一种遵循先入后出First In,Last Out的逻辑的线性数据结构。我们可以将栈类比为桌面上的一摞盘子,如果需要拿出底部的盘子,则需要先将上面的盘子依次取出。
栈常用操作
栈的常用操作如下表所示,具体的方法名需要根据所使用的编程语言来确定。我们以常见的push()、pop()、peek()命名为例。
| 方法 | 描述 | 时间复杂度 |
|---|---|---|
push() |
元素入栈(添加至栈顶) | O(1) |
pop() |
栈顶元素出栈 | O(1) |
peek() |
访问栈顶元素 | O(1) |
/* 初始化栈 */ |
栈简单实现
栈遵循先入后出的原则,因此只能在栈顶添加或删除元素。我们可以使用链表来实现栈。将链表的头节点视为栈顶,尾节点视为栈底。对于入栈操作,只需将元素插入链表头部,这种节点插入方法被称为“头插法”。而对于出栈操作,只需将头节点从链表中删除即可。



/* 基于链表实现的栈 */ |
5.2 队列
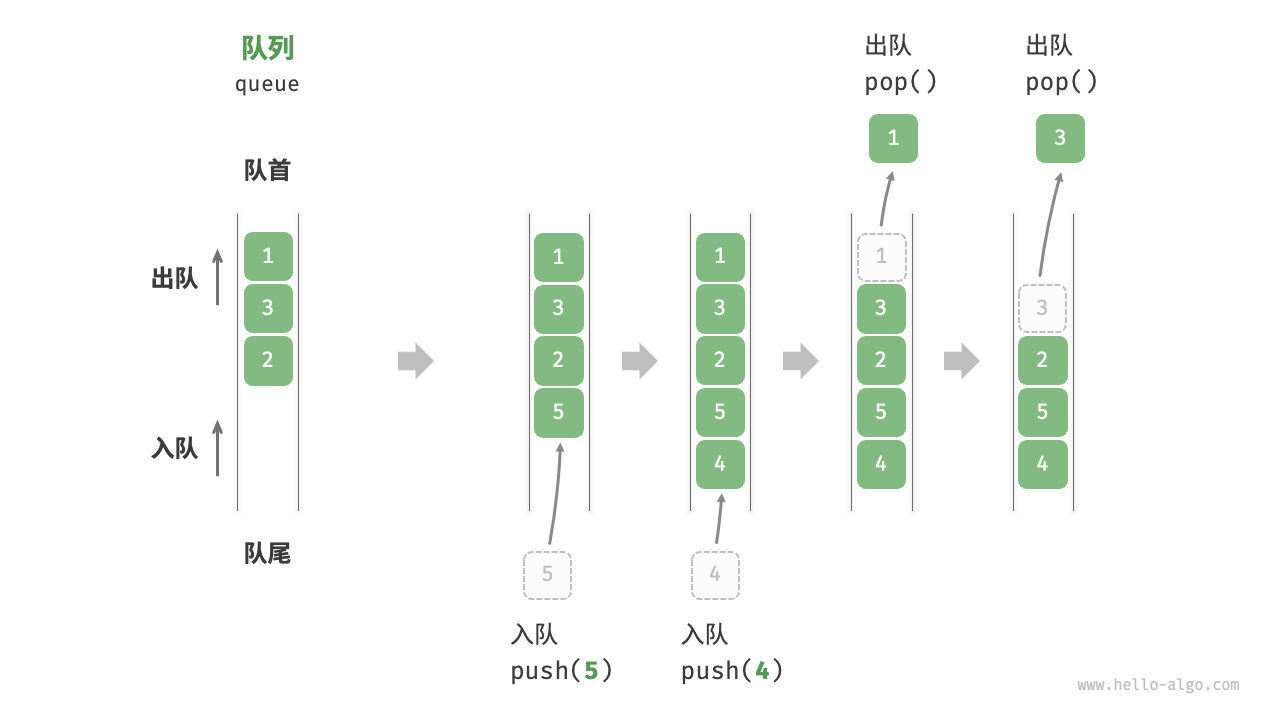
「队列 queue」是一种遵循先入先出First In, First Out规则的线性数据结构。顾名思义,队列模拟了排队现象,即新来的人不断加入队列的尾部,而位于队列头部的人逐个离开。
队列常用操作
队列的常用操作如下表所示,具体的方法名需要根据所使用的编程语言来确定。我们以常见的push()、pop()、peek()命名为例。
| 方法 | 描述 | 时间复杂度 |
|---|---|---|
push() |
元素入队,即将元素添加至队尾 | O(1) |
pop() |
队首元素出队 | O(1) |
peek() |
访问队首元素 | O(1) |
/* 初始化队列 */ |
队列简单实现
为了实现队列,需要一种数据结构,可以在一端添加元素,并在另一端删除元素。我们可以使用链表来实现队列。将链表的“头节点”和“尾节点”分别视为“队首”和“队尾”,规定队尾仅可添加节点,队首仅可删除节点。



/* 基于链表实现的队列 */ |
5.3 双向队列
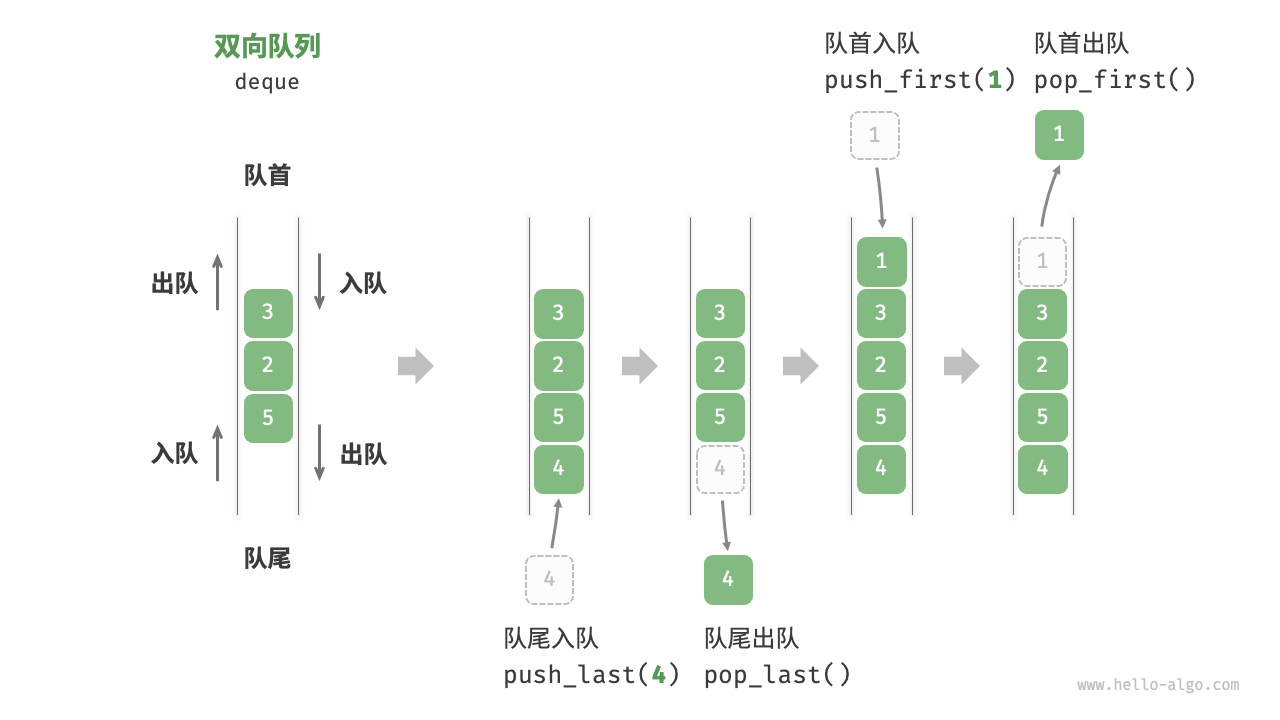
在队列中,我们仅能在头部删除或在尾部添加元素。如下图所示,「双向队列 deque」提供了更高的灵活性,允许在头部和尾部执行元素的添加或删除操作。
双向队列常用操作
双向队列的常用操作如下表所示。
| 方法 | 描述 | 时间复杂度 |
|---|---|---|
pushFirst() |
将元素添加至队首 | O(1) |
pushLast() |
将元素添加至队尾 | O(1) |
popFirst() |
删除队首元素 | O(1) |
popLast() |
删除队尾元素 | O(1) |
peekFirst() |
访问队首元素 | O(1) |
peekLast() |
访问队尾元素 | O(1) |
/* 初始化双向队列 */ |
双向队列简单实现
对于双向队列而言,头部和尾部都可以执行入队和出队操作。换句话说,双向队列需要实现另一个对称方向的操作。为此,我们采用“双向链表”作为双向队列的底层数据结构。





由于实现比较复杂,这里暂时不记实现方法。
6. 哈希表
6.1 哈希表
「哈希表 hash table」,通过建立键key与值value之间的映射,实现高效的元素查询。简单来说,向哈希表输入一个键key,就可以在O(1)时间内获取对应的值value。
如下图所示,给定n个学生,每个学生都有“姓名”和“学号”两项数据。假如我们希望实现“输入一个学号,返回对应的姓名”的查询功能,则可以采用下图所示的哈希表来实现。

除哈希表外,数组和链表也可以实现查询功能,它们的效率对比如下表所示。
| 数组 | 链表 | 哈希表 | |
|---|---|---|---|
| 查找元素 | O(n) |
O(n) |
O(1) |
| 添加元素 | O(1) |
O(1) |
O(1) |
| 删除元素 | O(n) |
O(n) |
O(1) |
观察发现,在哈希表中进行增删查改的时间复杂度都是O(1),非常高效。
哈希表常用操作
哈希表的常见操作包括,初始化、查询操作get(key)、添加键值对put(key, value)和删除键值对remove(key)等。
/* 初始化哈希表 */ |
哈希表有三种常用遍历方式,遍历键值对、遍历键和遍历值。
/* 遍历哈希表 */ |
哈希表简单实现
我们可以用数组来实现哈希表。在哈希表中,数组中的每个空位称为「桶 bucket」,每个桶可存储一个键值对。因此,查询操作就是找到key对应的桶,并在桶中获取value。
那怎么基于key来定位对应的桶呢?这是通过「哈希函数 hash function」实现的。在哈希表中输入一个key,可以通过哈希函数得到该key对应的键值对在数组中的存储位置。计算过程分为两步。
- 通过某种哈希算法
hash()计算得到哈希值。 - 将哈希值对桶数量(数组长度)
capacity取模,从而获取该key对应的数组索引index。
index = hash(key) % capacity |
随后,就可以利用index在哈希表中访问对应的桶,从而获取value。
设数组长度capacity = 100、哈希算法hash(key) = key,哈希函数为key % 100。下图以key学号和value姓名为例,展示了哈希函数的工作原理。
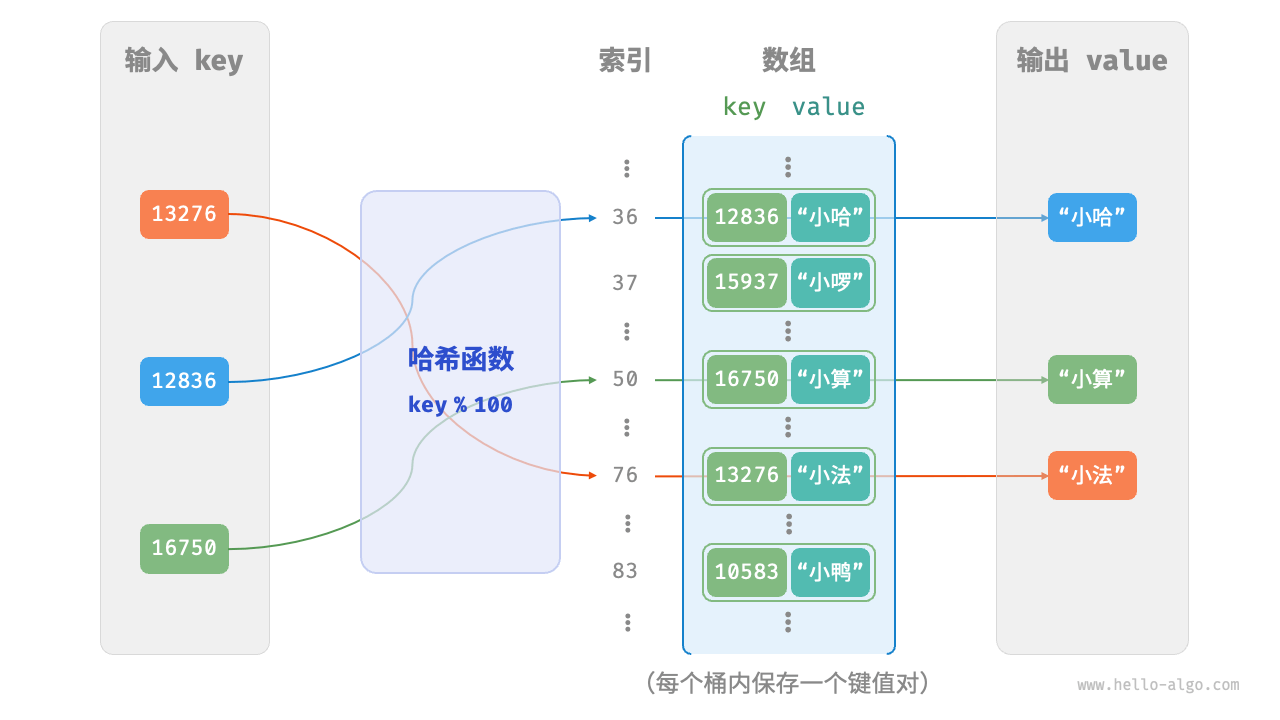
下面代码实现了一个简单哈希表。将key和value封装成一个类Pair,以表示键值对。
/* 键值对 */ |
哈希冲突与扩容
本质上看,哈希函数的作用是将所有key构成的输入空间映射到数组所有索引构成的输出空间,而输入空间往往远大于输出空间。因此,理论上一定存在“多个输入对应相同输出”的情况。
12836 % 100 = 36 |
如下图所示,两个学号指向了同一个姓名,这显然是不对的。我们将这种多个输入对应同一输出的情况称为「哈希冲突 hash collision」。
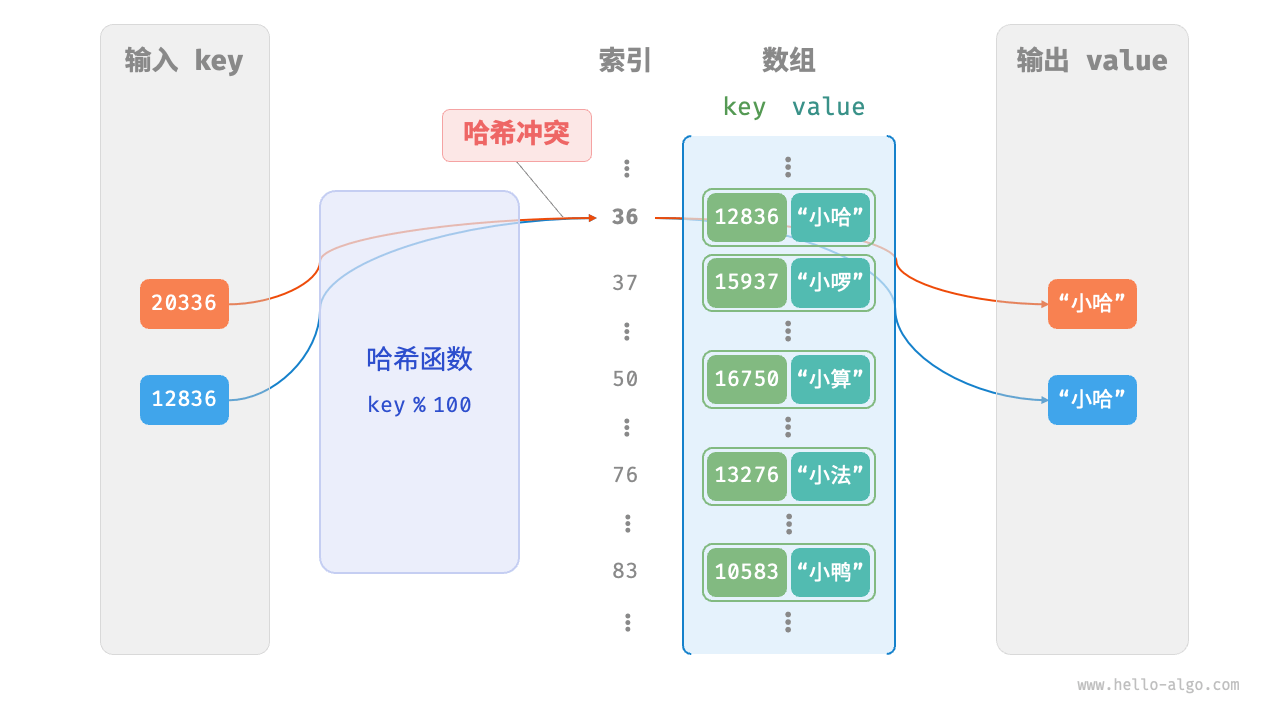
简单来说,可以通过扩容哈希表来减少哈希冲突。因为哈希表容量n越大,多个key被分配到同一个桶中的概率就越低,冲突就越少。如下图所示,扩容前键值对(136, A)和(236, D)发生冲突,扩容后冲突消失。

类似于数组扩容,哈希表扩容需将所有键值对从原哈希表迁移至新哈希表,非常耗时。并且由于哈希表容量capacity改变,需要通过哈希函数来重新计算所有键值对的存储位置,这进一步提高了扩容过程的计算开销。
由于哈希冲突和哈希算法比较复杂,这里就不做过多解释,可以自行阅读。
附录
文件还未上传 Github







